|
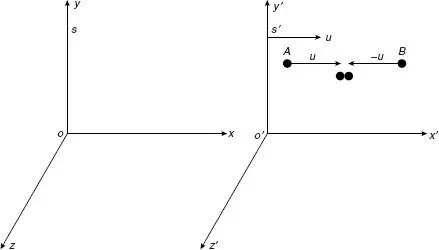
Consider two frames of
references S and S'. Further, S' is moving with constant
velocity v along X-direction. To explain the variation of mass
with velocity, consider the collision of two exactly similar balls A and B,
each of mass m, moving in opposite direction along X-axis with
equal speed u' in frame S'. After collision they coalesce into one
body.
Applying the, law of
conservation of momentum on the collision of the balls in frame s', we
have

After collision, the
coalesced mass must be at rest in frame S'. Hence, it moves with
velocity v in frame S. Let u1,u2 be the velocities
and m1, m2 be the masses of balls A and B, respectively, in
frame S. Using the law of addition of velocities, the above velocities
can be written as
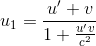 ......(1) ......(1)
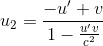 .....(2) .....(2)
Applying the law of
conservation of momentum on the collision of the balls in frame s, we
have
m1u1 + m2u2 =
(m1 + m2)v....(3)
Substituting u1 and u2 values
from Equations (1) and (2), we have
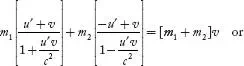
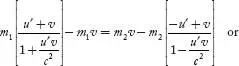

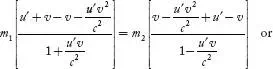
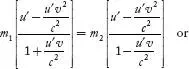
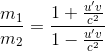 .........(4) .........(4)
The above equation
makes a relationship between the masses of balls in frame S and
their velocities in frame S'. Now, to obtain relation between masses of
balls and their velocities in frame S, we proceed as follows.
Squaring Equation (1)
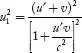
and using the above equation,
the value 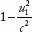 is is
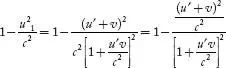
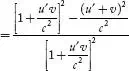
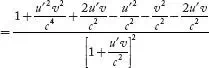
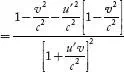
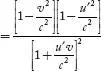
Therefore,
...(5)
Similarly, using equation
(2) we get
...(6)
Dividing Equation
(6) by Equation (5) and taking square root throughout, we have
...(7)
Comparing Equations
(4) and (7), we have
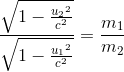 ....(8) ....(8)
Suppose, m2 is at
rest in frame s, then u2 = 0 and m2 = m0 (say)
where m0 is the rest mass of the ball B, thenEquation
(19.48) becomes
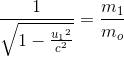 ....(9) ....(9)
As both the balls are
similar, hence the rest masses of both balls are the same, so we can write
the rest mass of m2 is equal to rest mass of m1, that is equal
to mo. Then, Equation (9) becomes
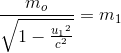 ....(10) ....(10)
Here, m1 is the
mass of ball A when it is moving with velocity u1 in frame s.
After collision, the coalescent mass containing mass of ball A moves with
velocity v in frame s.
In general, if we take the
mass of ball A as m, when it is moving with velocity v in
frame s, then
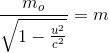 .......(11) .......(11)
where m0 is the
rest mass of the body and m is the effective mass.
Equation (11) is the
relativistic formula for the variation of mass with velocity. Here, we see
some special cases:
Case (i): When the
velocity of the body, v is very small compared to velocity of
height, c, then v2/c2 is negligible compared to one.
Therefore,
m = m0*
Case (ii): If the
velocity of the body v is comparable to the velocity of light c,
then 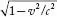 is less than one, so, m> mo. is less than one, so, m> mo.
The mass of a moving body
appears greater than its rest mass.
Case (iii): Suppose the
velocity of a body is equal to velocity of light, c, then, it
possess infinite mass.
The effective mass of
particles has been experimentally verified by using particle accelerators in
case of electrons and protons by increasing their velocities very close to
velocity of light.
|