Band Theory of Solids

Introduction

According to Quantum free Theory of methods a conduction E in a metal experiences constant (or zero) potential and free to move within the crystal but will not come out the metal. This theory successfully explains electrical conductivity, specific heat etc but fails to explain many other physical properties, for example (I) Difference between conductors, insulators and semiconductors.

To overcome the above problems, the periodic potentials due to +ve ions in a metal have been considered.

Electrons in a periodic potential –Bloch Theorem:

An E moves through + ve ions, it experiences varying potential. The potential of the E at the +ve ions site is zero and is maximum in between two +ve ions sites.

The potential experienced by an eˉ, then it passes though +ve ions shown in life.

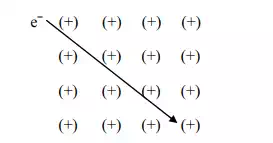
i.e The potential experienced by an E‟s in shown in Fig known as real periodic potential variation

To study the motion of E in lattice and the energy states it can occupy, Schrodinger equation is necessary

For making simplicity, Koenig-penny introduced a simple model for the shape of potential variation. The potential inside the crystal is approximated to the shape of rectangular steps.

KRONIG PENNY MODEL:-

Kronig – penny consider a periodic management of potential walls and barriers to represent the potential variation exhibited by the E , Known as Ideal-periodic square well potential as shown in figure. New forms of boundary conditions are developed to obtain a simple solution known as cyclic or periodic boundary conditions.

Conclusion From Kronig –Penny Model:

1).The Energy spectrum of E consists of an infinite number of allowed energy bonds separated by intervals in which, there are no allowed energy levels. These are known as forbidden regions.

2). When α a increase, the first term of eq(1) on LHS decrease , so that the width of the allowed energy bonds is increased and forbidden energy regions become narrow.

3). The width of the allowed bond decrease with the increase of p value. When p à α, the allowed energy regions become infinity narrow and the energy spectrum becomes line spectrum.

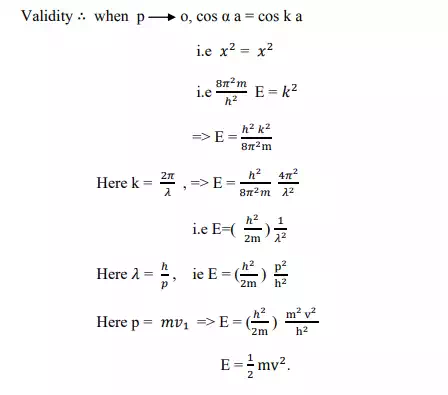
The wave functions associated with this model can be calculated by solving Schrödinger‟s eq for two regions 1 and 2.

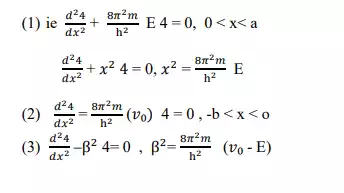
These two eq are solved by using Block and Koenig-penny models, and applying Boundary conditions the solution is