Energy levels – Fermi Dirac Distribution

According to the Quantum theory Quantization leads to discrete energy levels. The electrons are distribution among these energy levels according to Pauli’s exclusions principle it allows a maximum number of two electrons with spins in opposite directors in any energy level. The pair of electrons, one with sign up and the other with sign down occupy the lowest energy level. The next pair occupies the next level. This process goes on until all the electrons in the metal occupy their position.

But there will be many more allowed energy levels available for occupation. The highest energy level that can be occupied at ok is called Fermi energy level. I t is denoted by E f . When the metal is not under the influence of an external field, all the levels above the Fermi energy level are empty; those lying below are completely filled.

#Energy levels and order of filling levels in a metal.

The energy associated with Ef is called Fermi Energy.

The speed of the electron occupying the Fermi level is called Fermi Velocity.

Fermi – Dirac Distribution:

When the material is at a temperature higher than OK, it receives thermal energy from surroundings i.e. electrons are thermally excited. As a result, they move into the higher energy levels which are unoccupied at OK. The occupation obeys a statistical distribution called Fermi – Dirac distribution law.

 According to this distribution law, the probability f(E) that a given energy state E is occupied at a temperature T is given by

Here f(E) is called Fermi – Dirac probability function. It indicates that the fraction of all energy state (E) occupied under thermal equilibrium „K‟ is Boltzmann constant.

Expression for Fermi Energy level(Ef)

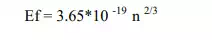
Where n is concentration of electrons.

Drawbacks of Quantum free electron theory :

(1) Lorentz Number : The Lorentz number in the Quantum free electron theory is given by

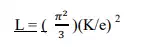
Here „K‟ is Boltzmann constant and „e‟ is charge of electron the observed Lorentz number is greater than the theoretical value as calculated from the above expression. i.e the Lorentz number is found to be vary with temperature. When metals are heated, the positive ions cores vibrate about their mean position and generate photons. The Phonons along with the free electrons carry some of the heat supplied to the metal. This must be the cause of large difference between observed and theoretical Lorentz number.

(2) Conductivity : According to Quantum free electron theory, the conductivity of a metal is

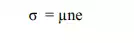
Here „µ‟ is the mobility of electron, „n‟ is the free electron concentration and „e‟ is the electron charge.

According to the above equation, polyvalent metals like Aluminium (Al) should be more conductive than mono valent metals like copper (cu). But experimentally it is not so.

(3) Hall co efficient: According to the free electron theory, the hall coefficients for all metals is negative whereas there are certain metals like Be, Cd, Zn for which the Hall coefficient is + ve

(4) Free electron theory could not explain why certain substances behave as insulators and some other substances as semiconductors, in spite of they have free electrons in them.