Relation Between Relaxation Time And Collision Time:-

Consider a conduction electron travelling inside a metal in the direction AB with a velocity `V` let it be scattered by

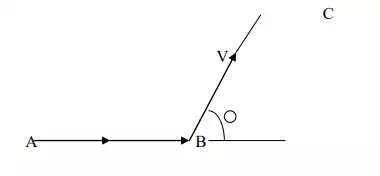
an ion core located by `B` as a result, the electron travels along BC With the same velocity making an angle `Q` with the Original Direction `Q` is called scattering angle.

The value of `Q` is likely to be different for different collisions. The average value of coso taken avers Avery large number of collisions is represented by . Then the relaxation time Tr is related to the mean collision time according to the relation.

If the scattering is equally possible is all directions (symmetric scattering) then the average scattering angle of a large number of scattering will be cosø =900 , then =0 and Tr = T. i.e. the mean collisions time can be treated as relaxation time itself.

Mean Free Path (˄):-

Let us consider S1, S2, and S3……. Etc are the free paths between the first, second, third etc. collisions, the mean free path `˄` is defined as the average of all the free paths.

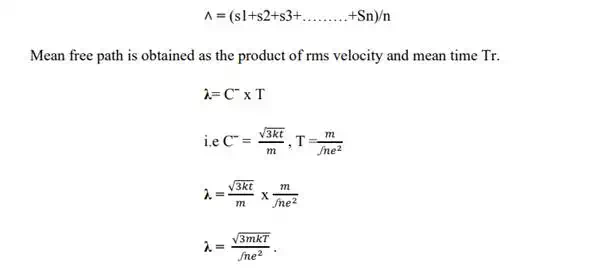
From the above expression, the resistibility `S` is Proportional to square root of temperature in according with classical theory. But experimentally it is no true.

Relation between relaxation time and mobility is

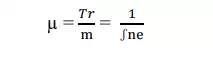
Drift Velocity Of An Electron In A Metal:-

When a current `I` is passed through a metallic wire, the electrons undergo multiple scattering with the + ve ions and move in a direction opposite to the current direction.

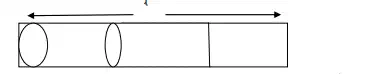
Let us consider a conductor of cross – sectional area `A` and length ʵ , so that גA is the volume of the conductor .if there are length `N` Number of electrons for unit volume of the metal, then the total number of electrons in the specimen in ` NLA`. If `E` is the charge of the electron , then the total charge `Q` due to all the free electrons in the sample.

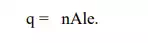
Let `t` be the time taken by the eˉ for moving from one end of the conductor to the other end. During this time, the charge crossed at any point in the conductor is q. the flowing through the conductor.

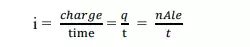
If v is the drift velocity of the electron, then the time required for the electron to move from one end to the other end is t= distance / velocity = l/v

The drift velocity increases with the increase of current density or current and decreases with the increase of electron concentration `n`