Heisenberg’s uncertainty principle

1. According to Classical mechanics, a moving particle at any instant has fixed position in space and definite momentum which can be determined simultaneously with any desired accuracy. This assumption is true for objects of appreciable size, but fails in particles of atomic dimensions.

2. Since a moving atomic particle has to be regarded as a de-Broglie wave group, there is a limit to measure particle properties.

3. According to Born probability interpretation, the particle may be found anywhere within the wave group moving with group velocity.

4. If the group is considered to be narrow, it is easier to locate its position, but the uncertainty in calculating its velocity and momentum increases.

5. If the group is wide, its momentum is estimated easily, but there is great uncertainty about the exact location of the particle.

Heisenberg a German scientist in 1927, gave uncertainty principle which states that

“The determination of exact position and momentum of a moving particle simultaneously is impossible’’.

In general, if △x represents the error in measurement of position of particle along xaxis, and △p represents error in measurement of momentum, then

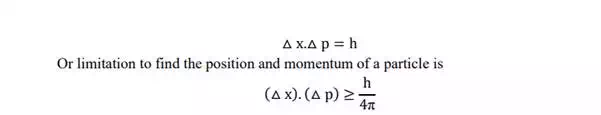
i.e Heisenberg uncertainty principle states that both the position and momentum cannot be measured simultaneously with perfect accuracy.

Particle in 1-Dimensional potential box:

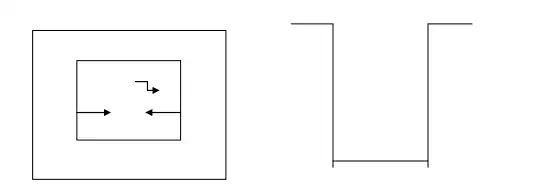
1. The wave nature of a moving particle leads to some remarkable consequences when the particle is restricted to a certain region of space instead of being able to move freely when a particle bounces back and forth between the walls of a box.

2. If one –dim motion of a particle is assumed to take place with zero potential energy over a fixed distance, and if the potential energy is assumed to become infinite at the extremities of the distance, it is described as a particle in a 1-D box, and this is the simplest example of all motions in a bound state.

3. The Schrodinger wave equation will be applied to study the motion of a particle in 1-D box to show how quantum numbers, discrete values of energy and zero point energy arises.

4. From a wave point of view, a particle trapped in a box is like a standing wave in a string stretched between the box‟s wall.

5. Consider a particle of mass „m‟moving freely along x- axis and is confined between x=0 and x= a by infinitely two hard walls, so that the particle has no chance of penetrating them and bouncing back and forth between the walls of a 1- D box.

6. If the particle does not lose energy when it collides with such walls, then the total energy remains constant.

7. This box can be represented by a potential well of width „a‟ ,where V is uniform inside the box throughout the length „a‟ i.e V= 0 inside the box or convenience and with potential walls of infinite height at x=0 and x=a, so that the PE „V‟ of a particle is infinitely high V=∞ on both sides of the box.

8. The boundary condition are

Normalization of wave function:

The wavefunctions for the motion of the particle are