Refraction by Lenses
We have already learned that a
lens is a carefully ground or molded piece of transparent material that
refracts light rays in such a way as to form an image. Lenses serve to refract
light at each boundary. As a ray of light enters a lens, it is refracted; and
as the same ray of light exits the lens, it is refracted again. The net effect
of the refraction of light at these two boundaries is that the light ray has
changed directions. Because of the special geometric shape of a lens, the light
rays are refracted such that they form images. Before we approach the topic of
image formation, we will investigate the refractive ability of
converging and diverging lenses.
How a Lens Refracts Light
First lets consider a double
convex lens. Suppose that several rays of light approach
the lens; and suppose that these rays of light are traveling parallel to the principal
axis. Upon reaching the front face of the lens,
each ray of light will refract towards the normal to the surface. At this
boundary, the light ray is passing from air into a more dense medium (usually
plastic or glass). Since the light ray is passing from a medium in which it
travels fast (less optically dense) into a
medium in which it travels relatively slow (more optically
dense), it will bend towards the normal line. This
is the FST principle of refraction. This is shown
for two incident rays on the diagram below. Once the light ray refracts across
the boundary and enters the lens, it travels in a straight line until it
reaches the back face of the lens. At this boundary, each ray of light will
refract away from the normal to the surface. Since the light ray is passing
from a medium in which it travels slow (more optically
dense) to a medium in which it travels fast (less optically
dense), it will bend away from the normal line; this
is the SFA principle of refraction.
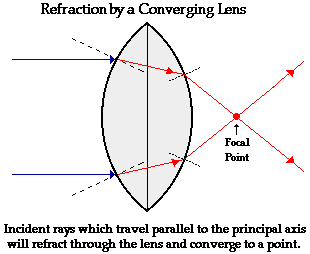
The above diagram shows the behavior of two incident rays approaching parallel
to the principal axis. Note that the two rays converge at a point; this point
is known as the focal point of the lens. The first generalization that can be
made for the refraction of light by a double convex lens is as follows:
|
Refraction Rule for a
Converging Lens Any incident ray traveling parallel to the principal axis of a converging lens will refract through the lens and travel through the focal point on the opposite side of the lens. |
Now suppose that the rays of light are traveling through the
focal point on the way to the lens. These rays of light will refract when they
enter the lens and refract when they leave the lens. As the light rays enter
into the more dense lens material, they
refract towards the normal; and as they exit into the less dense air, they
refract away from the normal. These specific rays will exit the lens traveling
parallel to the principal axis.
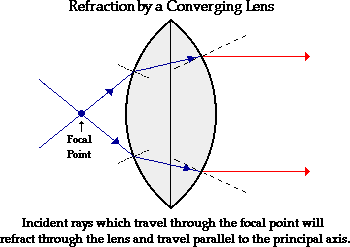
The above diagram shows the behavior of two incident rays traveling through
the focal point on the way to the lens. Note that the two rays refract parallel
to the principal axis. A second generalization for the refraction of light by a
double convex lens can be added to the first generalization.
|
Refraction Rules for a
Converging Lens · Any incident ray traveling parallel to
the principal axis of a converging lens will refract through the lens and
travel through the focal point on the opposite side of the lens. · Any incident ray traveling through the
focal point on the way to the lens will refract through the lens and travel
parallel to the principal axis. |
The Thin Lens Approximation
These two "rules" will greatly simplify the task of
determining the image location for objects placed in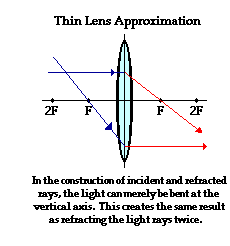
front of
converging lenses. This topic will be discussed in the next part of
Lesson 5. For now, internalize the meaning of the rules
and be prepared to use them. As the rules are applied in the construction of
ray diagrams, do not forget the fact that Snells' Law of refraction of light holds for each of
these rays. It just so happens that geometrically, when Snell's Law is applied
for rays that strike the lens in the manner described above, they will refract
in close approximation with these two rules. The tendency of incident light
rays to follow these rules is increased for lenses that are thin. For such thin
lenses, the path of the light through the lens itself contributes very little
to the overall change in the direction of the light rays. We will use this
so-called thin-lens approximation in this unit. Furthermore, to simplify the construction
of ray diagrams, we will avoid refracting each light ray twice - upon entering
and emerging from the lens. Instead, we will continue the incident ray to the
vertical axis of the lens and refract the light at that point. For thin lenses,
this simplification will produce the same result as if we were refracting the
light twice.
Rules
of Refraction for Diverging Lenses
Now let's investigate the refraction of light by double
concave lens. Suppose that several rays of light approach the lens; and suppose that
these rays of light are traveling parallel to the principal
axis. Upon reaching the front face of the lens,
each ray of light will refract towards the normal to the surface. At this
boundary, the light ray is passing from air into a more dense medium (usually
plastic or glass). Since the light ray is passing from a medium in which it
travels relatively fast (less optically dense) into a
medium in which it travels relatively slow (more optically
dense), it will bend towards the normal line. This
is the FST principle of refraction. This is shown
for two incident rays on the diagram below. Once the light ray refracts across
the boundary and enters the lens, it travels in a straight line until it
reaches the back face of the lens. At this boundary, each ray of light will
refract away from the normal to the surface. Since the light ray is passing
from a medium in which it travels relatively slow (more optically
dense) to a medium in which it travels fast (less optically dense), it will bend away from the normal line. This is the SFA
principle of refraction. These principles of refraction are identical
to what was observed for the double convex lens above.
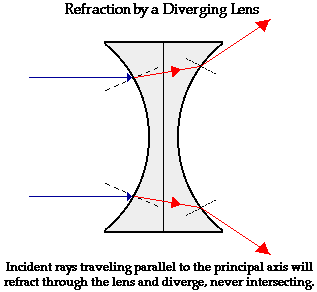
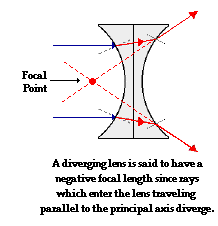The above diagram shows the behavior of two incident rays approaching parallel
to the principal axis of the double concave lens. Just like the double
convex lens above, light bends towards the normal when entering
and away from the normal when exiting the lens. Yet, because of the different
shape of the double concave lens, these incident rays are not converged to a
point upon refraction through the lens. Rather, these incident rays diverge
upon refracting through the lens. For this reason, a double concave lens can
never produce a real image. Double concave lenses produce images that are
virtual. This will be discussed in more detail in the next part of
Lesson 5. If the refracted rays are extended backwards
behind the lens, an important observation is made. The extension of the
refracted rays will intersect at a point. This point is known as the focal
point. Notice that a diverging lens such as this double concave lens does not
really focus the incident light rays that are parallel to the principal axis;
rather, it diverges these light rays. For this reason, a diverging lens is said
to have a negative focal length.
The first generalization can now be made for the refraction
of light by a double concave lens:
|
Refraction Rule for a
Diverging Lens Any incident ray traveling parallel to the principal axis of a diverging lens will refract through the lens and travel in line with the focal point (i.e., in a direction such that its extension will pass through the focal point). |
Now suppose that the rays of light are traveling
towards the focal point on the way to the lens. Because of the negative focal
length for double concave lenses, the light rays will head towards the focal
point on the opposite side of the lens. These rays will actually reach the lens
before they reach the focal point. These rays of light will refract when they
enter the lens and refract when they leave the lens. As the light rays enter
into the more dense lens material, they
refract towards the normal; and as they exit into the less dense air, they
refract away from the normal. These specific rays will exit the lens traveling
parallel to the principal axis.
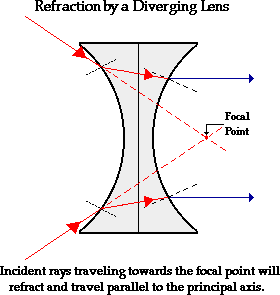
The above diagram shows the behavior of two incident rays traveling towards
the focal point on the way to the lens. Note that the two rays refract parallel
to the principal axis. A second generalization for the refraction of light by a
double concave lens can be added to the first generalization.
|
Refraction Rules for a
Diverging Lens · Any incident ray traveling
parallel to the principal axis of a diverging lens will refract through the
lens and travel in line with the focal point (i.e., in a
direction such that its extension will pass through the focal point). · Any incident ray traveling
towards the focal point on the way to the lens will refract through the lens
and travel parallel to the principal axis. |
A Third Rule of Refraction for Lenses
The above discussion focuses on the manner in which
converging and diverging lenses refract incident rays that are traveling
parallel to the principal axis or are traveling through (or towards) the focal
point. But these are not the only two possible incident rays. There are a
multitude of incident rays that strike the lens and refract in a variety of
ways. Yet, there are three specific rays that behave in a very predictable
manner. The third ray that we will investigate is the ray that passes through
the precise center of the lens - through the point where the principal axis and the
vertical axis intersect. This ray will refract as it enters and refract as it
exits the lens, but the net effect of this dual refraction is that the path of
the light ray is not changed. For a thin lens, the refracted
ray is traveling in the same direction as the incident ray and is approximately
in line with it. The behavior of this third incident ray is depicted in the diagram below.
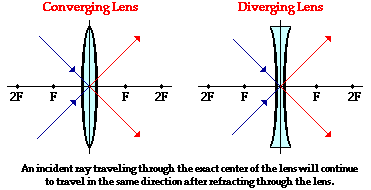
Now we have three incident rays whose
refractive behavior is easily predicted. These three rays lead to our three rules of
refraction for converging and diverging lenses. These three rules are
summarized below.
|
Refraction Rules for a
Diverging Lens · Any incident ray traveling parallel to
the principal axis of a diverging lens will refract through the lens and
travel in line with the focal point (i.e., in a
direction such that its extension will pass through the focal point). · Any incident ray traveling towards the
focal point on the way to the lens will refract through the lens and travel
parallel to the principal axis. · An incident ray that passes through
the center of the lens will in effect
continue in the same direction that it had when it entered the lens. |
These three rules of refraction for converging and diverging
lenses will be applied through the remainder of this lesson. The rules merely
describe the behavior of three specific incident rays. While there is a multitude of
light rays being captured and refracted by a lens, only two rays are needed in
order to determine the image location. So as we proceed with this lesson, pick
your favorite two rules (usually, the ones that are easiest to remember) and
apply them to the construction of ray diagrams and the determination of the
image location and characteristics.