Total Internal Reflection
A common Physics lab is to sight through the long side of an
isosceles triangle at a pin or other object held behind the opposite face. When
done so, an unusual observation - a discrepant event - is observed. The diagram
on the left below depicts the physical situation. A ray of light entered the
face of the triangular block at a right angle to the boundary. This ray of
light passes across the boundary without refraction since it was incident along
the normal (recall the If I Were An Archer Fish page). The
ray of light then travels in a straight line through the glass until it reaches
the second boundary. Now instead of transmitting across this boundary, all of
the light seems to reflect off the boundary and transmit out the opposite face
of the isosceles triangle. This discrepant event bothers many as they spend
several minutes looking for the light to refract through the second boundary.
Then finally, to their amazement, they looked through the third face of the
block and clearly see the ray. What happened? Why did light not refract through
the second face?
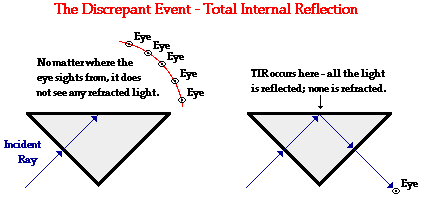
The phenomenon observed in this part of the lab is known as
total internal reflection. Total internal reflection, or TIR as it is intimately called, is the reflection of the total amount of
incident light at the boundary between two media. TIR is the topic of focus in
Lesson 3.
To understand total internal reflection, we will begin with a
thought experiment. Suppose that a laser beam is submerged in a tank of water
(don't do this at home) and pointed upwards towards water-air boundary. Then
suppose that the angle at which the beam is directed upwards is slowly altered,
beginning with small angles of incidence and proceeding towards larger and
larger angles of incidence. What would be observed in such an experiment? If we
understand the principles of boundary behavior,
we would expect that we would observe both reflection and refraction. And
indeed, that is what is observed (mostly). But that's not the only observation
that we could make. We would also observe that the intensity of the reflected
and refracted rays do not remain constant. At angle of incidence close to 0
degrees, most of the light energy is transmitted across the boundary and very
little of it is reflected. As the angle is increased to greater and greater
angles, we would begin to observe less refraction and more reflection. That is,
as the angle of incidence is increased, the brightness of the refracted ray
decreases and the brightness of the reflected ray increases. Finally, we would
observe that the angles of the reflection and refraction are not equal. Since
the light waves would refract away from the normal (a case of the SFA
principle of refraction), the angle of refraction would be greater
than the angle of incidence. And if this were the case, the angle of refraction
would also be greater than the angle of reflection (since the angles of
reflection and incidence are the same). As the angle of incidence is increased,
the angle of refraction would eventually reach a 90-degree angle. These
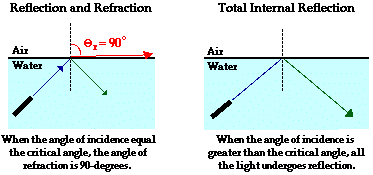
principles are depicted in the diagram below.
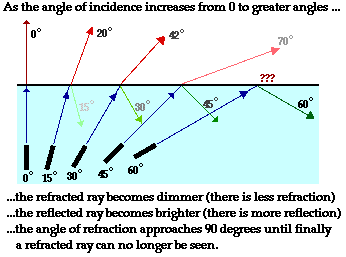
The maximum possible angle of refraction is 90-degrees. If
you think about it (a practice that always helps), you recognize that if the
angle of refraction were greater than 90 degrees, then the refracted ray would
lie on the incident side of the medium - that's just not possible. So in the
case of the laser beam in the water, there is some specific value for the angle
of incidence (we'll call it the critical angle) that yields an angle of refraction of 90-degrees. This particular
value for the angle of incidence could be calculated using Snell's Law (ni = 1.33, nr = 1.000,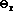 
= 90
degrees, 
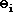= ???) and would be found to be 48.6 degrees. Any
angle of incidence that is greater than 48.6 degrees would not result in
refraction. Instead, when the angles of incidence is greater than 48.6 degrees
(the critical angle), all of the energy (the total energy) carried
by the incident wave to the boundary stays within the water (internal to the original medium) and undergoes reflection off the
boundary. When this happens, total internal reflection occurs.
Two
Requirements for Total Internal Reflection
Total internal reflection (TIR) is the phenomenon that
involves the reflection of all the incident light off the boundary. TIR only
takes place when both of the following two conditions are met:
· the light is in the more dense medium and
approaching the less dense medium.
· the angle of incidence is greater than the
so-called critical angle.
Total internal reflection will not take place unless the
incident light is traveling within the more optically
dense medium towards the less optically dense medium.
TIR will happen for light traveling from water towards air, but it will not
happen for light traveling from air towards water. TIR would happen for light
traveling from water towards air, but it will not happen for light traveling
from water (n=1.333) towards crown glass (n=1.52). TIR occurs because the angle
of refraction reaches a 90-degree angle before the angle of incidence reaches a
90-degree angle. The only way for the angle of refraction to be greater than
the angle of incidence is for light to bend away from the normal. Since light
only bends away from the normal when passing from a more dense medium into a
less dense medium, then this would be a necessary condition for total internal
reflection.
Total internal reflection only occurs with large angles of
incidence. Question: How large is large? Answer: larger than the critical
angle. As mentioned above, the critical angle for the water-air boundary is
48.6 degrees. So for angles of incidence greater than 48.6-degrees, TIR occurs.
But 48.6 degrees is the critical angle only for the water-air boundary. The
actual value of the critical angle is dependent upon the two materials on
either side of the boundary. For the crown glass-air boundary, the critical
angle is 41.1 degrees. For the diamond-air boundary, the critical angle is 24.4
degrees. For the diamond-water boundary, the critical angle is 33.4 degrees.
The critical angle is different for different media. In the next part of
Lesson 3, we will investigate how to determine the
critical angle for any two materials. For now, let's internalize the idea that
TIR can only occur if the angle of incidence is greater than the critical angle
for the particular combination of materials.
Light Piping
and Optical Fibers
Total internal reflection is often demonstrated in a Physics
class through a variety of demonstrations. In one such demonstration, a beam of
laser light is directed into a coiled plastic thing-a-ma
jig. The plastic served as a light pipe, directing the light through the coils until it finally exits out the
opposite end. Once the light entered the plastic, it was in the more dense medium.
Every time the light approached the plastic-air boundary, it is approaching at
angles greater than the critical angle. The two conditions necessary for TIR
are met, and all of the incident light at the plastic-air boundary stays
internal to the plastic and undergoes reflection. And with the room lights off,
every student becomes quickly aware of the ancient truth that Physics is better
than drugs.
This demonstration helps to illustrate the
principle by which optical fibers work. The
use of a long strand of plastic (or other material such as glass) to pipe light
from one end of the medium to the other is the basis for modern day use of optical fibers. Opticalfibers are
used in communication systems and micro-surgeries. Since total internal
reflection takes place within the fibers, no
incident energy is ever lost due to the transmission of light across the
boundary. The intensity of the signal remains constant.
Another common Physics demonstration involves the use of a
large jug filled with water and a laser beam. The jug has a pea-sized hole
drilled in its side such that when the cork is removed from the top of the jug,
water begins to stream out the jug's side. The beam of laser light is then
directed into the jug from the opposite side of the hole, through the water and
into the falling stream. The laser light exits the jug through the hole but is
still in the water. As the stream of water begins to fall as a projectile along
a parabolic path to the ground, the laser light becomes trapped within the
water due to total internal reflection. Being in the more dense medium
(water) and heading towards a boundary with a less dense medium (air), and
being at angles of incidence greater than the critical angle, the light never
leaves the stream of water. In fact, the stream of water acts as a light pipe
to pipe the laser beam along its trajectory. Once more, students viewing the
demonstration are convinced of the fact that Physics is better than drugs.
Flickr Physics Photo
Laser light shown passing into a
hemi-cylindrical dish filled with water. The light enters the water (at the
curved side of the dish) along the normal line; no bending occurs upon entry.
The light continues through the water along a straight line until it reaches
the boundary with air (at the flat side of the dish). The angle of incidence in
the water is 50°. Since the angle of incidence is greater the air-water
critical angle of about 48°, it undergoes total internal reflection (TIR).
Rather than refract out of the dish of water at the flat side, the laser light
is seen reflecting and exiting along the curved side of the dish.
Check Your Understanding
1. For each combination of media, which light ray (A or B)
will undergo total internal reflection if the incident angle is gradually
increased?
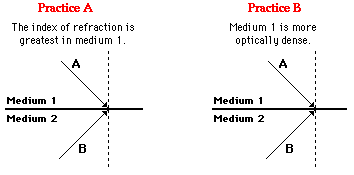
Practice A: Light ray A is in the more
dense medium and it will be the one which will undergo TIR.
Practice B: Light
ray A is in the more dense medium and it
will be the one which will undergo TIR.