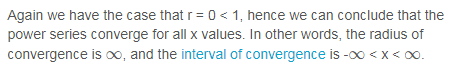Root test
Let there be a series \sigma a_{n}σan. Then we say that:
![]() Formula 2: Root test
Formula 2: Root test
Where:
If r < 1, then the series is convergent
If r > 1 (including infinity), then the series is divergent
If r = 1, then the series could either be divergent or convergent.
Basically if r=1, then the root test fails and would require a different test to determine the convergence or divergence of the series. Realize that these rules are exactly the same as the ratio test! Again, I am not going to provide a proof that the root test works, but I will post a link here showing the proof:
http://people.sju.edu/~pklingsb/pfroot.pdf
Let's look at an example of using the root test!
Consider the following series:
· 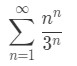 Equation 3: Divergence Root test pt. 1
Equation 3: Divergence Root test pt. 1
· First we set:
![]() Equation 3: Divergence Root test pt. 2
Equation 3: Divergence Root test pt. 2
· Now using the root test, we will have that:
![]() Equation 3: Divergence Root test pt. 3
Equation 3: Divergence Root test pt. 3
· Notice that we can factor the power of n in both the denominator and numerator so that:
![]() Equation 3: Divergence Root test pt. 4
Equation 3: Divergence Root test pt. 4
· We can even factor the power of n out of the absolute value so that:
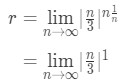 Equation 3: Divergence Root test pt. 5
Equation 3: Divergence Root test pt. 5
· Now taking the limit of this as nn→\infty∞ will result in r being infinity. In other words,
![]() Equation 3: Divergence Root test pt. 6
Equation 3: Divergence Root test pt. 6
· Since r = \infty∞ >1, then we know that the series is divergent.
Since we very familiar with the ratio test and root test now, let us talk about finding the interval of convergence.
How to find interval of convergence
We are able to find the interval of convergence of a power series. Power series are in the form
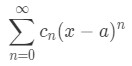 Formula 3: Power Series
Formula 3: Power Series
Where c_{n}cn are the coefficients of each term in the series and a is a number the series is centred around. We are able to find the radius and interval of convergence if we take either the ratio test or the root test. Depending on the power series, one test may be more convenient than the other. How do we find the interval of convergence using the ratio test?
Let
![]() Formula 4: Interval of Convergence pt. 1
Formula 4: Interval of Convergence pt. 1
Then applying the ratio test will give:
![]()
Formula 4: Interval of Convergence pt. 2
After taking the limit, set r < 1 and then manipulate the inequality so that it takes the form of |x-a| < R, where R is the radius of convergence.
The interval of convergence is the value of all x's, for which the power series converges. This interval will be
![]()
Formula 4: Interval of Convergence pt. 3
It is also important to check the endpoints of this inequality (-R+a and R+a) to see if they converge as well. If it is, then include them into the inequality!
Note that there are some cases in which we cannot get the inequality |x-a| < R. You might just end up getting r = 0 < 1. This means that for all x values, r = 0. Hence, the radius of convergence is \infty∞ and the interval of convergence is -\infty∞ < x < \infty∞. You also might get a case where r = \infty∞. In that case, the power series is always divergent for all x.
Alright, now that we know what the radius and interval of converge is, why don't we do a few examples?
Let's take a look at the power series:
· 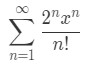 Equation 4: Ratio test Interval of Convergence pt. 1
Equation 4: Ratio test Interval of Convergence pt. 1
· Since we see factorials, it will be more convenient to use the ratio test here. Let
![]() Equation 4: Ratio test Interval of Convergence pt. 2
Equation 4: Ratio test Interval of Convergence pt. 2
· Then,
![]() Equation 4: Ratio test Interval of Convergence pt. 3
Equation 4: Ratio test Interval of Convergence pt. 3
· Applying the ratio test formula gives us:
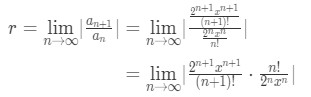
Equation 4: Ratio test Interval of Convergence pt. 4
· Matching the powers and the factorials will give us:
![]()
Equation 4: Ratio test Interval of Convergence pt. 5
· See here that we can cancel some of the powers so that:
![]()
Equation 4: Ratio test Interval of Convergence pt. 6
· Expanding the factorials out will lead to lots of terms cancelling:
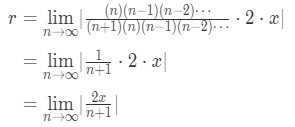
Equation 4: Ratio test Interval of Convergence pt. 7
· We can factor x out of the absolute value so that:
![]()
Equation 4: Ratio test Interval of Convergence pt. 8
· Notice that we have to put an absolute value around the x when factoring it out of the absolute value. Now taking the limit will give us:
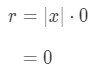
Equation 4: Ratio test Interval of Convergence pt. 9
You may see that this is not in the form |x-a| < R. However notice that r = 0 < 1 for all x values. This means that for all x values, the power series converges. Hence the radius of convergence is infinity, and the interval of convergence is -\infty∞ < x < \infty∞ (because it converges everywhere).
How do we find the interval of convergence using the root test?
Well again, we just use the root test formula and set r<1and try to get the inequality |x-a| interval of convergence will be. Don't forget to check the endpoints to see if the series is convergent or divergent. If it is convergent, then include it in the interval.
Notice again that you will encounter cases where you will end up either getting r = 0 < 1 or r = \infty∞. r = 0 implies the power series is convergent for all x values, and r = \infty∞ implies the power series is divergent always.
Now let us take a look at a case where we find the interval of convergence using the root test. Consider the power series:
· 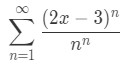 Equation 5: Root test Interval of Convergence pt. 1
Equation 5: Root test Interval of Convergence pt. 1
· We want to use root test here because we see a lot of powers of n. So let
![]() Equation 5: Root test Interval of Convergence pt. 2
Equation 5: Root test Interval of Convergence pt. 2
· Recall that the root test formula is
![]() Equation 5: Root test Interval of Convergence pt. 3
Equation 5: Root test Interval of Convergence pt. 3
· Hence we will get:
![]() Equation 5: Root test Interval of Convergence pt. 4
Equation 5: Root test Interval of Convergence pt. 4
· Factoring the powers of n out in the absolute value gives:
![]() Equation 5: Root test Interval of Convergence pt. 5
Equation 5: Root test Interval of Convergence pt. 5
· Notice that we can factor the power of n outside of the absolute value so that
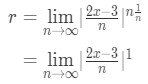 Equation 5: Root test Interval of Convergence pt. 6
Equation 5: Root test Interval of Convergence pt. 6
· We can factor 2x-3 out of the absolute value so that:
![]() Equation 5: Root test Interval of Convergence pt. 7
Equation 5: Root test Interval of Convergence pt. 7
· Taking the limit will yield the result:
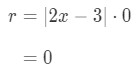 Equation 5: Root test Interval of Convergence pt. 8
Equation 5: Root test Interval of Convergence pt. 8