Radius Of A Circle And Chord
Radius of a circle
A circle can be defined as the locus of a point moving in a plane, in such a manner that its distance from a fixed point is always constant. The fixed point is known as the center of the circle and distance between any point on the circle and its center is called the radius of a circle.
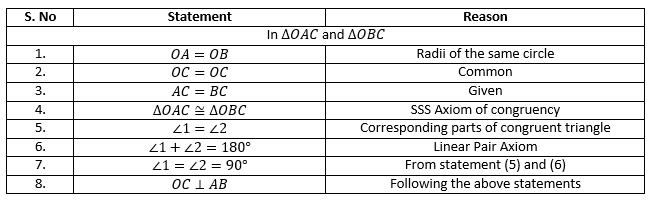
Given a line and a Circle, it could either be touching the circle, interesting line or non-touching.
Consider any line AB and a circle. Then according to the relative positions of the line and the circle, three possibilities can arise as shown in the given figure.

Line AB intersects the given circle at two distinct points P and Q. The line AB in this case is referred to as secant of the circle. Points P and Q lie on the circumference of the circle, but they do not pass through the center of the circle ‘O’, hence line segment PQ is known as a chord of the circle as its endpoints lie on the circle.
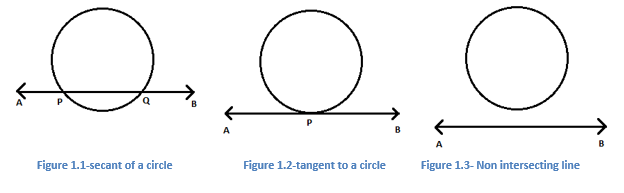
Therefore the chord of a circle can be defined as a line segment joining any two distinct points on the circle’s circumference. A chord passing through the center of a circle is known as the diameter of the circle and it is the largest chord of the circle. This diameter is twice that of the radius of a circle i.e. D=2r, where ‘D’ is the diameter and ‘r’ is the radius.
Radius of a circle = Diameter/2
Or
Diameter of a circle = 2 x Radius
Let us discuss a few important theorems and their proofs related to the chord of a circle.
Chord of a Circle Theorems
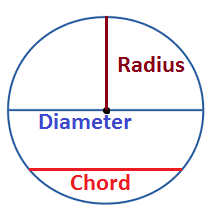
Theorem 1: The perpendicular line drawn from the center of a circle to a chord bisects the chord.
Given: AB= Chord; OC⊥AB
To prove: AC=BC
Construction: Draw OA and OB
Proof:
S. No. | Statement | Reason |
In ΔOAC and ΔOBC | ||
1 | OA = OB | Radii of the same circle |
2 | OC = OC | Common |
3 | ∠OCA = ∠OCB | Each angle measure 90 degrees |
4 | ΔOAC ≅ ΔOBC | By RHS congruence criterion |
5 | AC = CB | By CPCT (Corresponding parts of congruent triangles) |
The converse of the above theorem is also true.
Theorem 2: The line drawn through the centre of the circle to bisect a chord is perpendicular to the chord.
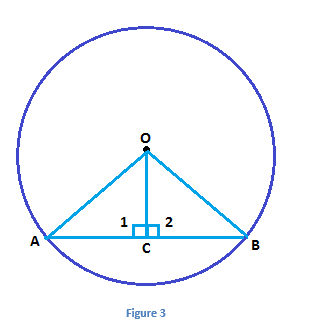
Given: C is the midpoint of the chord AB of the circle with centre of circle at O
To prove:OC⊥AB
Construction: Join OA, OB and OC
Proof: