Ratio Test
Convergence tests are used to find the convergence of series or power series. There are many tests for convergence, but in this article we are going to focus on the ratio test. Ratio test is one of the tests used to determine the convergence or divergence of infinite series. You can even use the ratio test to find the radius and interval of convergence of power series! Many students have problems of which test to use when trying to find whether the series converges or diverges. We recommend you to use this series test if your series appear to have factorials or powers.
The definition of the ratio test is the following:
Let there be a series \Sigma a_{n}Σan. Then we say that:
![]()
Formula 1: Ratio test
Where:
If r < 1, then the series is convergent. A converging series means that the infinite series has a finite sum.
If r > 1 (including infinity), then the series is divergent. This means the infinite series sums up to infinity.
If r = 1, then the series could either be divergent or convergent.
Basically if r = 1, then the ratio test fails and would require a different test to determine the convergence or divergence of the series. I am not going to provide a proof as to why the ratio test works, but this link here provides a step by step formal proof of it.
http://blogs.ubc.ca/infiniteseriesmodule/appendices/proof-of-the-ratio-test/proof-of-the-ratio-test/
Why don't we take a look at some ratio test examples and learn how to fully utilize the ratio test.
Ratio test for convergence
Let's take a look at the following series:
· 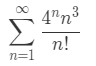 Equation 1: Convergence Ratio test pt. 1
Equation 1: Convergence Ratio test pt. 1
· Let's see whether the series converges or diverges. Right away, you see a factorial in the series. This means that ratio test is recommended. Let
![]() Equation 1: Convergence Ratio test pt. 2
Equation 1: Convergence Ratio test pt. 2
· So then we will also have
![]()
Equation 1: Convergence Ratio test pt. 3
· Using these two and plugging them into the ratio test formula will give us:
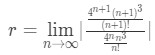
Equation 1: Convergence Ratio test pt. 4
· We know that when you are dividing a fraction, then that is the same as multiplying the reciprocal of the fraction. Thus, we can change this to
![]()
Equation 1: Convergence Ratio test pt. 5
· What I like to do is match all the numerators and denominators I see here. Notice that I can match the powers, factorials and polynomials so that it looks like this:
![]()
Equation 1: Convergence Ratio test pt. 6
· Notice that the powers from the 4's can cancel. Hence this will give us:
![]()
Equation 1: Convergence Ratio test pt. 7
· Also, the cube of the polynomials can be factored. Doing so leads to
![]()
Equation 1: Convergence Ratio test pt. 8
· In addition, we can use the factorial rules to expand out the factorials. Doing all of this will give us:
![]()
Equation 1: Convergence Ratio test pt. 9
· Notice that expanding the factorials leads all the terms to cancel except or n+1 in the denominator. Hence, we can conclude that simplifying factorials leads to:
![]()
Equation 1: Convergence Ratio test pt. 10
· Within the brackets, we are going to divide the n+1 by n, and so we will end up with
![]()
Equation 1: Convergence Ratio test pt. 11
· Now we are actually going to take the limit here. Notice that as nn→\infty∞, \frac{1}{(n+1)}(n+1)1 goes to 0. In addition, The 1+\frac{1}{n}1+n1 inside the brackets will become 1. Nevertheless, it will be multiplied by 0, so the entire limit will go to 0. Therefore
![]() Equation 1: Convergence Ratio test pt. 12
Equation 1: Convergence Ratio test pt. 12
We know that 0 < 1, so what does the ratio test conclude? It concludes that the series converge. Note that using the ratio test does not tell you the sum of the series; you would have to use some other means to do that.Now let's take a look at a case in which the ratio test says the series diverges.
Ratio test for divergence
Let's test for divergence in the following series:
· 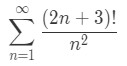
· Equation 2: Divergence Ratio test pt. 1
· Again we see the factorial, so it will be wise to use the ratio test.
Let
![]()
Equation 2: Divergence Ratio test pt. 2
· So we will have that:
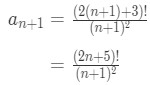
Equation 2: Divergence Ratio test pt. 3
· Hence using the ratio test formula will give us:
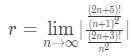
Equation 2: Divergence Ratio test pt. 4
· Again we can simply this so that we don't have a fraction on top of a fraction. Instead we can change this to multiplying by the reciprocal of the fraction. This gives us:
![]()
Equation 2: Divergence Ratio test pt. 5
· Let's match the polynomials and the factorials so that we have
![]()
Equation 2: Divergence Ratio test pt. 6
· We can expand out the factorials so that
![]()
Equation 2: Divergence Ratio test pt. 7
· Notice that the terms can cancel so that we can simply the equation to:
![]()
Equation 2: Divergence Ratio test pt. 8
· Multiplying the fractions together and expanding the denominator will give us:
![]()
Equation 2: Divergence Ratio test pt. 9
· Factoring n^{2}n2 out of the denominator leads to:
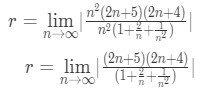
Equation 2: Divergence Ratio test pt. 10
· Now we should be able to take the limit as nn→\infty∞. Notice that taking the limit leads to the denominator becoming 1, and the numerator goes to infinity. Hence the entire limit goes to infinity. Hence we can conclude that:
![]() Equation 2: Divergence Ratio test pt. 11
Equation 2: Divergence Ratio test pt. 11
· Since \infty∞ > 1, then we can conclude that the series goes to infinity.
If you want to look at more examples of ratio tests with converging or diverging series, click the lesson tab. While we are talking about ratio test, we might as well talk about the root test as well. Why? Because they are very similar!