Functional dependence; conformal mapping

We start once more with a differentiable transformation,

defined in some domain D. In the previous section we concentrated chiefly on the case where the Jacobian was different from zero at all points in D. We wish now to consider the other extreme, namely those transformations F for which the Jacobian is zero at every point of D. Let us start with the special case in which F is linear,

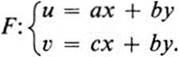
Then

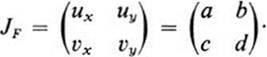
Thus the Jacobian is everywhere equal to zero if and only if the determinant of the linear transformation F is equal to zero. We have seen in Sect. 14 that a linear transformation with zero determinant maps the whole plane into a straight line through the origin. Thus, for linear transformations, the property that the Jacobian is everywhere zero is equivalent to the geometrical property that the whole plane is mapped into some straight line.

Returning to the general transformation (18.1), we ask what it means for F to map the whole domain D into a line through the origin. The equation of such a line is λu + μυ = 0, where λ and μ are constants, and the condition that Fmaps D into that line is that λf(x, y) + μg(x, y) ≡ 0 in D. The following terminology is used.

Definition 18.1 Two functions f(x, y) and g(x, y) defined in a domain D are linearly dependent if there exist numbers λ, μ, not both zero, such that

(See Ex. 18.3c for an alternative characterization of linear dependence.)

Lemma 18.1If F is a differentiable transformation defined by Eq. (18.1), and if f and g are linearly dependent, then the Jacobian of F is identically zero.

PROOF. Differentiating Eq. (18.2) yields

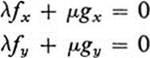
at every point of D. This is a pair of simultaneous linear homogeneous equations for the unknowns λ and μ, whose matrix is the Jacobian matrix of F at a given point of D. If the Jacobian of F were different from zero at some point, then the determinant of this system would be different from zero, and there would be a unique solution λ = 0, μ = 0. But by assumption, λ and μ are not both zero. Hence, the Jacobian must vanish at each point. 

Now the notion of linearly dependent functions is a special case of the general concept of functional dependence. Intuitively, functional dependence means that there is some relation between the functions f and g. For our purposes the following definition is most appropriate.

Definition 18.2 Two functions f(x, y), g(x, y) defined in a domain D are functionally dependent if there exists a continuously differentiable function φ(u, υ) such that

1. φ(f(x, y), g(x, y)) ≡ 0.

2. ∇φ ≠ 0 at each point (u, υ) = f(x, y), g(x, y)) for (x, y) in D.

RemarkGeometrically, functional dependence has the following interpretation. Condition 1 means that the transformation F defined by Eq. (18.1) maps the domain D into the set of points satisfying φ(u, υ) = 0, and Condition 2 tells us (by the implicit function theorem) that this set of points lies on a regular curve (Fig. 18.1). (See the note in Ex. 18.5b for further comments on the definition.)

Example 18.1

Here Condition 1 is just Eq. (18.2), and Condition 2 says that not both λ and μ are zero, so that f and g are linearly dependent.

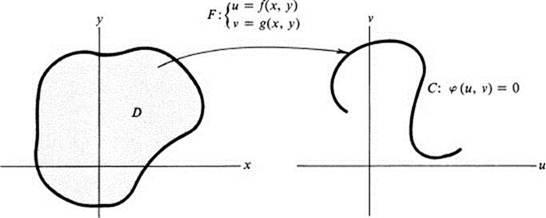
FIGURE 18.1 Geometrical interpretation of functional dependence

Example 18.2

Let

Then

This means that Condition 1 is fulfilled if we set

Condition 2 is also fulfilled, since

Thus xy and 1 + x²y² are functionally dependent.

Theorem 18.1 Let F be a differentiable transformation defined by Eq.(18.1) . If f(x, y) and g(x, y) are functionally dependent, then the Jacobian of F is identically zero.

PROOF. If we differentiate the equation of Condition 1, using the chain rule, we find

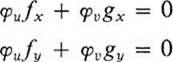
at every point. Using Condition 2, the reasoning of Lemma 18.1 may be applied without change. 

It is natural to ask whether the converse of Th. 18.1 is true. If the Jacobian of a mapping vanishes identically, does that imply functional dependence? The answer is that this is more or less true, but not without qualifications. Rather than go into detail, we may summarize the situation as follows. Given a pair of functions f(x, y), g(x, y), which we should like to test for functional dependence, the first step is to compute the Jacobian. If the Jacobian is notidentically zero, then f and g are not functionally dependent by Th. 18.1. On the other hand, if the Jacobian is identically zero, then this is strong evidence of functional dependence, and the best procedure is to try to find an explicit relationship between the functions. (See also the Remark preceding Ex. 18.27.)

Example 18.3

Let

Are these functionally dependent?

We start by finding the Jacobian,

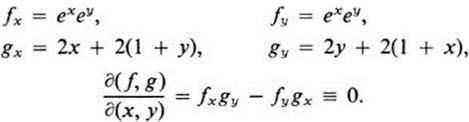
Thus we are led to seek a functional relationship. By elementary manipulations we can rewrite f and g in the form,

Thus

so that f and g are funcionally dependent.