Functional dependence between two variables

Two variables x and y are tied by a functional dependence, if for each value of one of them it is possible to receive by the certain rule one or some values of another.

E x a m p l e .

A temperature T of water boiling and atmosphere pressure p are tied by a functional dependence,
because each value of pressure corresponds to a certain value of the temperature and inversely.
So, if p = 1 bar, then T = 100°C; if p = 0.5 bar, then T = 81.6°C.

A variable, values of which are given, is called an argument or an independent variable; the other variable, values of which are found by the certain rule is called a function. Usually an argument is marked as x, and a function is marked as y . If only one value of function corresponds to each value of argument, this function is called a single-valued function; otherwise, if there are many corresponding values, this function is called a multiple-valued function ( two-valued, three-valued and etc.).

E x a m p l e .

A body is thrown upwards; h is its height over a ground, t is the time, passed from a throwing moment.
h is a single-valued function of t, but t is a two-valued function of h, because the body is on the same
height twice: the first time at an assent, the second time at a fall. The formula

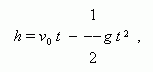
binding variables h and t ( initial velocity v₀ and an acceleration of a gravity g are constants here ), shows that we have only one value of h at the given t , and two values of t at the given h ( they are determined by solving the quadratic equation ).