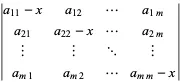
(1)
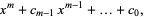
(2)
Cayley-Hamilton Theorem
Given
|
|
| (1) |
|
|
| (2) |
then
| (3) |
where 
is the identity matrix. Cayley verified this identity for 
and 3 and postulated that it was true for all 
. For 
, direct verification gives
|
|
| (4) |
|
|
| (5) |
|
|
| (6) |
|
|
| (7) |
|
|
| (8) |
|
|
| (9) |
|
|
| (10) |
|
|
| (11) |
so
| (12) |
The Cayley-Hamilton theorem states that an 
matrix 
is annihilated by its characteristic polynomial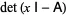 
, which is monic of degree .
