
(1)
Separation of variables method
Separation of variables is a method of solving ordinary and partial differential equations.
For an ordinary differential equation
| (1) |
where ![]() is nonzero in a neighborhood of the initial value, the solution is given implicitly by
is nonzero in a neighborhood of the initial value, the solution is given implicitly by
| (2) |
If the integrals can be done in closed form and the resulting equation can be solved fo
r ![]() (which are two pretty big "if"s), then a complete solution to the problem has been obtained. The most important equation for which this technique applies is
(which are two pretty big "if"s), then a complete solution to the problem has been obtained. The most important equation for which this technique applies is ![]() , the equation for exponential growth and decay (Stewart 2001).
, the equation for exponential growth and decay (Stewart 2001).
For a partial differential equation in a function 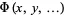 and variables
and variables ![]() ,
, ![]() , ..., separation of variables can be applied by making a substitution of the form
, ..., separation of variables can be applied by making a substitution of the form
| (3) |
breaking the resulting equation into a set of independent ordinary differential equations, solving these
for ![]() ,
, ![]() , ..., and then plugging them back into the original equation.
, ..., and then plugging them back into the original equation.
This technique works because if the product of functions of independent variables is a constant, each function must separately be a constant. Success requires choice of an appropriate coordinate system and may not be attainable at all depending on the equation. Separation of variables was first used by L'Hospital in 1750. It is especially useful in solving equations arising in mathematical physics, such as Laplace's equation, the Helmholtz differential equation, and the Schrödinger equation.