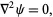
(1)
Laplace equation
The scalar form of Laplace's equation is the partial differential equation
| (1) |
where ![]() is the Laplacian.
is the Laplacian.
Note that the operator ![]() is commonly written as
is commonly written as ![]() by mathematicians (Krantz 1999, p. 16). Laplace's equation is a special case of the Helmholtz differential equation
by mathematicians (Krantz 1999, p. 16). Laplace's equation is a special case of the Helmholtz differential equation
| (2) |
with ![]() , or Poisson's equation
, or Poisson's equation
| (3) |
with ![]() .
.
The vector Laplace's equation is given by
| (4) |
A function ![]() which satisfies Laplace's equation is said to be harmonic. A solution to Laplace's equation has the property that the average value over a spherical surface is equal to the value at the center of the sphere (Gauss's harmonic function theorem). Solutions have no local maxima or minima. Because Laplace's equation is linear, the superposition of any two solutions is also a solution.
which satisfies Laplace's equation is said to be harmonic. A solution to Laplace's equation has the property that the average value over a spherical surface is equal to the value at the center of the sphere (Gauss's harmonic function theorem). Solutions have no local maxima or minima. Because Laplace's equation is linear, the superposition of any two solutions is also a solution.
A solution to Laplace's equation is uniquely determined if (1) the value of the function is specified on all boundaries (Dirichlet boundary conditions) or (2) the normal derivative of the function is specified on all boundaries (Neumann boundary conditions).
Coordinate System | Variables | Solution Functions |
Cartesian |
| exponential functions, circular functions, hyperbolic functions |
circular cylindrical |
| Bessel functions, exponential functions, circular functions |
conical |
| ellipsoidal harmonics, power |
confocal ellipsoidal |
| ellipsoidal harmonics of the first kind |
elliptic cylindrical |
| Mathieu function, circular functions |
oblate spheroidal |
| Legendre polynomial, circular functions |
parabolic |
| Bessel functions, circular functions |
parabolic cylindrical |
| parabolic cylinder functions, Bessel functions, circular functions |
paraboloidal |
| circular functions |
prolate spheroidal |
| Legendre polynomial, circular functions |
spherical |
| Legendre polynomial, power, circular functions |
Laplace's equation can be solved by
separation of variables in all 11 coordinate systems that the Helmholtz differential equation can. The form these solutions take is summarized in the table above. In addition to these 11 coordinate systems, separation can be achieved in two additional coordinate systems by introducing a multiplicative factor. In these coordinate systems, the separated form is
| (5) |
and setting
| (6) |
where ![]() are scale factors, gives the Laplace's equation
are scale factors, gives the Laplace's equation
| (7) |
If the right side is equal to 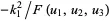 , where
, where ![]() is a constant and
is a constant and ![]() is any function, and if
is any function, and if
| (8) |
where ![]() is the Stäckel determinant, then the equation can be solved using the methods of the Helmholtz differential equation. The two systems where this is the case are bispherical and toroidal, bringing the total number of separable systems for Laplace's equation to 13 (Morse and Feshbach 1953, pp. 665-666).
is the Stäckel determinant, then the equation can be solved using the methods of the Helmholtz differential equation. The two systems where this is the case are bispherical and toroidal, bringing the total number of separable systems for Laplace's equation to 13 (Morse and Feshbach 1953, pp. 665-666).
In two-dimensional bipolar coordinates, Laplace's equation is separable, although the Helmholtz differential equation is not.
Zwillinger (1997, p. 128) calls
| (9) |
the Laplace equations.