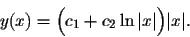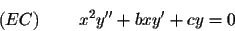
Euler-Cauchy Equations

An Euler-Cauchy equation is

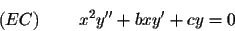
where b and c are constant numbers. Let us consider the change of variable

x = e^t.

Then we have

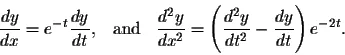
The equation (EC) reduces to the new equation

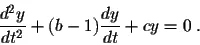
We recognize a second order differential equation with constant coefficients. Therefore, we use the previous sections to solve it. We summarize below all the cases:

(1)

Write down the characteristic equation

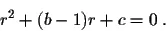
(2)

If the roots r₁ and r₂ are distinct real numbers, then the general solution of (EC) is given by

y(x) = c₁ |x|^r₁ + c₂ |x|^r₂.

(2)

If the roots r₁ and r₂ are equal (r₁ = r₂), then the general solution of (EC) is

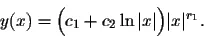
(3)

If the roots r₁ and r₂ are complex numbers, then the general solution of (EC) is

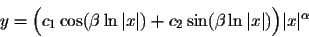
where 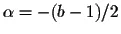 and .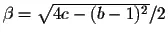

Example: Find the general solution to

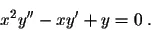
Solution: First we recognize that the equation is an Euler-Cauchy equation, with b=-1 and c=1.

1

Characteristic equation is r² -2r + 1=0.

2

Since 1 is a double root, the general solution is