Taylor’s series
A Taylor series is a series expansion of a function about a point. A one-dimensional Taylor series is an expansion of a real function ![]() about a point
about a point ![]() is given by
is given by
| (1) |
If ![]() , the expansion is known as a Maclaurin series.
, the expansion is known as a Maclaurin series.
Taylor's theorem (actually discovered first by Gregory) states that any function satisfying certain conditions can be expressed as a Taylor series.
The Taylor (or more general) series of a function ![]() about a point
about a point ![]() up to order
up to order ![]() may be found using Series[f,
may be found using Series[f, ![]() x, a, n
x, a, n![]() ]. The
]. The ![]() th term of a Taylor series of a function
th term of a Taylor series of a function ![]() can be computed in the Wolfram Language using SeriesCoefficient[f,
can be computed in the Wolfram Language using SeriesCoefficient[f, ![]() x, a, n
x, a, n![]() ] and is given by the inverse Z-transform
] and is given by the inverse Z-transform
| (2) |
Taylor series of some common functions include
|
|
| (3) |
|
|
| (4) |
|
|
| (5) |
|
|
| (6) |
|
|
| (7) |
|
|
| (8) |
To derive the Taylor series of a function ![]() , note that the integral of the
, note that the integral of the ![]() st derivative
st derivative ![]() of
of ![]() from the point
from the point ![]() to an arbitrary point
to an arbitrary point ![]() is given by
is given by
| (9) |
where ![]() is the
is the ![]() th derivative of
th derivative of ![]() evaluated at
evaluated at ![]() , and is therefore simply a constant. Now integrate a second time to obtain
, and is therefore simply a constant. Now integrate a second time to obtain
| (10) |
where ![]() is again a constant. Integrating a third time,
is again a constant. Integrating a third time,
| (11) |
and continuing up to ![]() integrations then gives
integrations then gives
| (12) |
Rearranging then gives the one-dimensional Taylor series
|
|
| (13) |
|
|
| (14) |
Here, ![]() is a remainder term known as the Lagrange remainder, which is given by
is a remainder term known as the Lagrange remainder, which is given by
| (15) |
Rewriting the repeated integral then gives
| (16) |
Now, from the mean-value theorem for a function ![]() , it must be true that
, it must be true that
| (17) |
for some 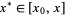 . Therefore, integrating
. Therefore, integrating ![]() times gives the result
times gives the result
| (18) |
(Abramowitz and Stegun 1972, p. 880), so the maximum error after ![]() terms of the Taylor series is the maximum value of (18) running through all
terms of the Taylor series is the maximum value of (18) running through all 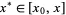 . Note that the Lagrange remainder
. Note that the Lagrange remainder ![]() is also sometimes taken to refer to the remainder when terms up to the
is also sometimes taken to refer to the remainder when terms up to the ![]() st power are taken in the Taylor series (Whittaker and Watson 1990, pp. 95-96).
st power are taken in the Taylor series (Whittaker and Watson 1990, pp. 95-96).
Taylor series can also be defined for functions of a complex variable. By the Cauchy integral formula,
|
|
| (19) |
|
|
| (20) |
|
|
| (21) |
In the interior of ![]() ,
,
| (22) |
so, using
| (23) |
it follows that
|
|
| (24) |
|
|
| (25) |
Using the Cauchy integral formula for derivatives,
| (26) |
An alternative form of the one-dimensional Taylor series may be obtained by letting
| (27) |
so that
| (28) |
Substitute this result into (◇) to give
| (29) |
A Taylor series of a real function in two variables ![]() is given by
is given by
| (30) |
This can be further generalized for a real function in ![]() variables,
variables,
| (31) |
Rewriting,
| (32) |
For example, taking ![]() in (31) gives
in (31) gives
| (33) |
| (34) |
Taking ![]() in (32) gives
in (32) gives
| (35) |
or, in vector form
| (36) |
The zeroth- and first-order terms are ![]() and
and 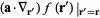 , respectively. The second-order term is
, respectively. The second-order term is
|
|
| (37) |
|
|
| (38) |
so the first few terms of the expansion are
|