Line Integral

Line integrals (also referred to as path or curvilinear integrals) extend the concept of simple integrals (used to find areas of flat, two-dimensional surfaces) to integrals that can be used to find areas of surfaces that "curve out" into three dimensions, as a curtain does. Note that related to line integrals is the concept of contour integration; however, contour integration typically applies to integration in the complex plane.

A line integral allows for the calculation of the area of a surface in three dimensions.

Line integrals have a variety of applications. For example, in electromagnetics, they can be used to calculate the work done on a charged particle traveling along some curve in a force field represented by a vector field. Or, in classical mechanics, they can be used to calculate the work done on a mass mm moving in a gravitational field. Both of these problems can be solved via a generalized vector equation.

Line integrals allow you to find the work done on particles moving in a vector force field.

Or, for example, a line integral could determine how much radiation a pirate would be exposed to from a radiation source near the path to his treasure.

Note that at different points along his path he will be exposed to different amounts of radiation depending on how close he is to the source. Integrating the radiation at every point via a line integral will help determine the total radiation the pirate is exposed to.

Or one might want to figure out how many calories a swimmer might burn in swimming along a certain route, where the currents in all areas can be accurately predicted.

This also would require the use of a line integral because the total work he needs to do will vary depending on the strength and direction of the current. So, a line integral over the path shown above will help determine the total work (or calories) that a swimmer will burn in swimming along the path.

Line Integrals - Fundamental Concepts

For a simple integral, the area is calculated under a curve defined by y = f(x):y=f(x):

Simple integral

To evaluate the area under the curve, one simply integrates f(x)f(x) from aa to b:b:

\text{Area} = \int_{a}^{b}f(x)\, dx.Area=∫ab​f(x)dx.

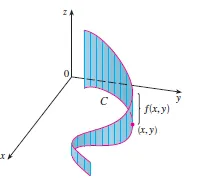
However, for line integrals, the area is a two-dimensional surface that "curves into three dimensions." It is wavy like a curtain rather than being completely flat like the example above:

Line integral

This is done by introducing the following set of parametric equations to define the curve CC in the xy-plane: