Green’s theorem

The idea behind Green's theorem

represents the circulation of FF around CC. If FF were the velocity field of water flow, for example, this integral would indicate how much the water tends to circulate around the path in the direction of its orientation.

One way to compute this circulation is, of course, to compute the line integral directly. But, if our line integral happens to be in two dimensions (i.e., FF is a two-dimensional vector field and CC is a closed path that lives in the plane), then Green's theorem applies and we can use Green's theorem as an alternative way to calculate the line integral.

Green's theorem transforms the line integral around CC into a double integral over the region inside CC. However, it's not obvious what function we should integrate over the region inside CC so that we still get the same answer as the line integral. The notion of circulation can aid us in determining what this function should be.

Think of the integral ∫CF⋅ds∫CF⋅ds as the “macroscopic” circulation of the vector field FF around the path CC. Now, imagine you came up with a “microscopic” version of circulation around a curve. This microscopic circulation at a point (x,y)(x,y) has to tell you how much FF would circulate around a tiny closed curve centered around (x,y)(x,y). We could picture the microscopic circulation as a bunch of small closed curves (shown below in green), where each curve respresents the tendency for the vector field to circulate at that location (imagine that the small curves were really, really small, much smaller than pictured).

Green's theorem is simply a relationship between the macroscopic circulation around the curve CC and the sum of all the microscopic circulation that is inside CC. If CC is a simple closed curve in the plane (remember, we are talking about two dimensions), then it surrounds some region DD (shown in red) in the plane. DD is the “interior” of the curve CC.

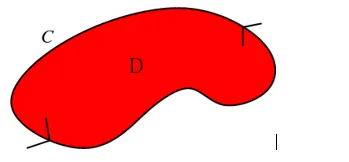
Green's theorem says that if you add up all the microscopic circulation inside CC (i.e., the microscopic circulation in DD), then that total is exactly the same as the macroscopic circulation around CC.

“Adding up” the microscopic circulation in DD means taking the double integral of the microscopic circulation over DD. Therefore, we can write Green's theorem as