Algebra of Matrices 

Algebra of Matrices is the branch of mathematics, which deals with the vector spaces between different dimensions. The innovation of matrix algebra came into existence because of n-dimensional planes present in our coordinate space.

A matrix (plural: matrices) is an arrangement of numbers, expressions or symbols in a rectangular array. This arrangement is done in horizontal-rows and vertical-columns, having an order of number of rows x number of columns. Every pair of points in a Three-dimensional space represent a unique equation with one or more than one solution.

The basic idea or the central idea of applied mathematics revolves around Linear Algebra. For instance, by reliving the rules and regulations or rather say Axioms, we get into a generalization of vector space, which by calculus leads to the Solution of Differential Equations.

Algebra of Matrix

Algebra of matrix involves the operation of matrices, such as Addition, subtraction, multiplication etc.

Let us understand the operation of the matrix in a much better way-

Addition/Subtraction of Matrices

Two matrices can be added/subtracted, iff (if and only if) the number of rows and columns of both the matrices are same, or the order of the matrices are equal.

For addition/subtraction, each element of the first matrix is added/subtracted to the elements present in the 2nd matrix.

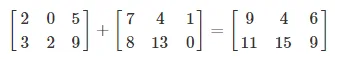
Example:

Matrix Multiplication

Like Matrix can be Multiplied two ways,

(i) Scalar Multiplication

(ii) Multiplication with another matrix

• Scalar Multiplication – It involves multiplying a scalar quantity to the matrix. Every element inside the matrix is to be multiplied by the scalar quantity to form a new matrix.

For example-

Rule of Matrix Algebra

The algebra of matrix follows some rules for addition and multiplication. Let us consider A, B and C are three different square matrices. A’ is the transpose and A^-1 is the inverse of A. I is the identity matrix and R is a real number.
Now as per the rules of laws of matrices:

• A+B = B+A →Commutative Law of Addition
• A+B+C = A +(B+C) = (A+B)+C →Associative law of addition
• ABC = A(BC) = (AB)C →Associative law of multiplication
• A(B+C) = AB + AC →Distributive law of matrix algebra
• R(A+B) = RA + RB

Also, see here rules for transposition of matrices:

• (A’)’ = A
• (A+B)’ = A’+B’
• (AB)’ = B’A’
• (ABC) = C’B’A’

The inverse rules of matrices are as follows:

• AI = IA = A
• AA^-1 = A^-1A = I
• (A^-1)^-1 = A
• (AB)^-1 = B^-1A^-1
• (ABC)^-1 = C^-1B^-1A^-1
• (A’)^-1 = (A^-1)’