Homogeneous Difference Equations
Now the general form of any second-order difference equation is:
![\[af(n+2)+b f(n+1) +cf(n) = d.\]](8_files/image001.webp)
Also, 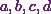 are
constants.
are
constants.
If  ,
then the equation becomes
,
then the equation becomes
![\[f(n+2)+a f(n+1) +bf(n) = 0.\]](8_files/image004.webp)
Then this is an example of second-order homogeneous difference equations.
Now Iíll show how to solve these type of equations.
METHOD
First of all, Iíll
choose a general solution to this difference equation. So, letís say 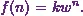
Next, Iíll put this
value of  in the difference equation.
in the difference equation.
So it will be
![\[kw^{n+2}+akw^{n+1}+bkw^{n} =0.\]](8_files/image007.webp)
Here  is
the common term.
is
the common term.
So I can take it out.
Thus the equation will be
![\[kw^{n}(w^2+aw+b) = 0.\]](8_files/image009.webp)
Since  cannot
be
cannot
be  ,
,  can be
can be  .
.
Therefore what I get is
![\[(w^2+aw+b) = 0.\]](8_files/image012.webp)
Now, this is the characteristic equation of this difference equation.
Next, I have to solve
this equation to get the values of  .
.
Since  has
the power
has
the power  , Iíll get two values of
, Iíll get two values of  .
.
So letís choose  and
and  .
.
Then the general solution of the difference equation will be
![\[f(n) = A \times m_1^{n} + B \times m_2^{n}.\]](8_files/image017.webp)
Now thatís how it works.
EXAMPLE
According to Stroud
and Booth (2013)* ďSolve the following difference equation: 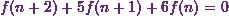 where
where 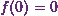 and
and 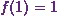 .Ē
.Ē
SOLUTION
Now here the given difference equation is
![\[ \boxed{f(n+2)+5f(n+1)+6f(n) = 0,~~~~~f (0) = 0, f(1) = 1.} \]](8_files/image021.webp)
First of all, Iíll choose the general solution of this equation as
![\[f(n) = kw^n.\]](8_files/image022.webp)
Now Iíll find out the characteristic equation of this difference equation.
STEP 1
So, for that Iíll
put 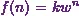 in the difference equation to get
in the difference equation to get
![\[kw^{n+2}+5kw^{n+1}+6kw^{n} = 0.\]](8_files/image024.webp)
Now I can take
out  as a common term. Therefore the new equation will be
as a common term. Therefore the new equation will be
![\[kw^n(w^2+5w+6) = 0.\]](8_files/image026.webp)
Since  cannot
be
cannot
be  ,
,  can be
can be  .
.
Therefore what I get is
![\[(w^2+5w+6) = 0.\]](8_files/image028.webp)
So the characteristic equation of this difference equation will be
![\[ \boxed{w^2+5w+6 = 0.} \]](8_files/image029.webp)
Next, Iíll solve this equation to get the general solution of the difference equation.
STEP 2
So I can factorise this characteristic equation as
![\[(w+2)(w+3) = 0.\]](8_files/image030.webp)
Thus the values
of  will be
will be 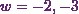 .
.
Hence the general solution of the difference equation is
(1) 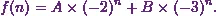
Now Iíll get the
values of 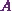 and
and  .
.
So Iíll
substitute  in the equation (1) to get
in the equation (1) to get
![\[f(0) = A \times (-2)^{0}+B\times (-3)^{0}.\]](8_files/image036.webp)
Now I already
know that 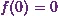 .
.
So this equation will be
![\[0 = A \times 1 + B \times 1.\]](8_files/image038.webp)
(2) 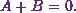
Next, Iíll
substitute 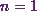 in the equation (1) to get
in the equation (1) to get
![\[f(1) = A \times (-2)^{1}+B\times (-3)^{1}.\]](8_files/image041.webp)
Now I already
know that 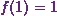 .
.
So this equation will be
![\[1 = A \times (-2) + B \times (-3).\]](8_files/image043.webp)
(3) 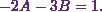
As I can see
from equation (2), 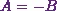 .
.
Next, Iíll put
back 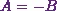 in equation (3).
in equation (3).
Thus it will be
![\[-2 (-B) -3 B = 1.\]](8_files/image046.webp)
So this gives 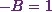 which
means
which
means
![\[B = -1.\]](8_files/image048.webp)
Hence the value
of 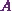 will be
will be
![\[A = 1.\]](8_files/image049.webp)
Now Iíll
substitute 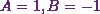 in the equation (1) to get
in the equation (1) to get
![\[f (n) = 1 \times (-2)^{n}+(-1)\times (-3)^{n}.\]](8_files/image051.webp)
So this means
![\[f (n) = (-2)^{n}- (-3)^{n}\]](8_files/image052.webp)
is the general solution of the difference equation.
Hence I can conclude that this is the answer to this example.