Gauss-Jordan Method To Find Out The Inverse Of A Matrix

 

Let’s say I have a matrix 

  \[ \textbf{A} = \begin{pmatrix} a_{11}&a_{12}\\ a_{21}&a_{22} \end{pmatrix} .\]

And I want to find out the inverse of this matrix.

Now, to get the inverse of the matrix 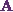\textbf{A}, I will follow a few steps.

First of all, I will find out the determinant of the matrix.

Next, I will determine the cofactor of each element of the matrix.

Then I’ll write to them in a matrix form.

In the end, I will find out the transpose of the new matrix.

And then only I can get the inverse of the matrix 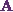\textbf{A} by using another formula.

GAUSS-JORDAN METHOD

Now in the Gauss-Jordan method, I’ll include the unit matrix \textbf{I} on the right-hand side. So the resultant matrix will look like

  \[ [\textbf{A}\qquad \textbf{I}]= \begin{pmatrix} a_{11}&a_{12}&|&1&0\\ a_{21}&a_{22}&|&0&1 \end{pmatrix}.\]

And my aim is to bring the unit matrix on the left-hand side. And for that, I have to use row operations on this matrix.

As per the Gauss-Jordan method, the matrix on the right-hand side will be the inverse of the matrix 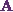\textbf{A}.

Now I’ll give some examples of how to use the Gauss-Jordan method to find out the inverse of a matrix.

EXAMPLE 1

According to Kreyszig (2005)*, “Find the inverse by Gauss-Jordan.

  \[ \begin{pmatrix} 3&-1&~~1\\ 15&~~6&-5\\ 5&-2&~~2 \end{pmatrix} .\]

”

SOLUTION

Now here the given matrix is 

  \[ \begin{pmatrix} 3&-1&~~1\\ 15&~~6&-5\\ 5&-2&~~2 \end{pmatrix} .\]

First of all, I’ll give it a name, say 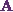\textbf{A}. Therefore the given matrix is 

  \[ \textbf{A} = \begin{pmatrix} 3&-1&~~1\\ 15&~~6&-5\\ 5&-2&~~2 \end{pmatrix} .\]

Now I’ll use the Gauss-Jordan method to find out the inverse of the matrix 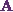\textbf{A}.

As per the Gauss-Jordan method, I’ll include the unit matrix \textbf{I} on the right-hand side like 

  \[ [\textbf{A}\qquad \textbf{I}]= \begin{pmatrix} 3&-1 & ~~1&|&1&0&0\\ 15&~~6&-5&|&0&1&0\\ 5&-2&~~2&|&0&0&1 \end{pmatrix}.\]

And my aim is to bring the unit matrix on the left-hand side. As per the Gauss-Jordan method, the matrix on the right-hand side will be the inverse of the matrix 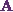\textbf{A}.

STEP 1

First of all, I’ll add 5 times row 1 to row 2. Simultaneously, I’ll subtract twice row 1 from row 3.

In mathematical form, I’ll write like:

  \[\text{Row}~ 2 + 5~ \text{Row}~ 1, ~~~\text{Row}~ 3 - 2~\text{Row}~ 1.\]

So the resultant matrix is 

  \[ [\textbf{A}\qquad \textbf{I}]= \begin{pmatrix} ~~3&-1 &1&|&~~1&0&0\\ ~~0&~~1&0&|&~~5&1&0\\ -1&~~0&0&|&-2&0&1 \end{pmatrix}.\]

As I can see, I have already got the identity matrix component at the second row.

Now I’ll try to bring the other two as well.

STEP 2

Next, I’ll multiply the row 3 of the matrix [\textbf{A}\qquad \textbf{I}] with (-1).

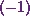So in mathematical form, it will be:

  \[\text{Row}~ 3 \times (-1).\]

Then the resultant matrix is 

  \[ [\textbf{A}\qquad \textbf{I}]= \begin{pmatrix} 3&-1 &1&|&1&0&~~0\\ 0&~~1&0&|&5&1&~~0\\ 1&~~0&0&|&2&0&-1 \end{pmatrix}.\]

Now I’ll interchange row 1 and 3 to get the resultant matrix as 

  \[ [\textbf{A}\qquad \textbf{I}]= \begin{pmatrix} 1&~~0 &0&|&2&0&-1\\ 0&~~1&0&|&5&1&~~0\\ 3&-1&1&|&1&0&~~0\end{pmatrix}.\]

Now I have got the identity matrix component at the first row as well.

Next, I’ll do that with the third row too.

STEP 3

Now I’ll subtract 3 times row 1 from row 3.

So in mathematical form, it will be:

  \[\text{Row}~3 - 3~\text{Row}~ 1.\]

Then the resultant matrix will be 

  \[ [\textbf{A}\qquad \textbf{I}]= \begin{pmatrix} 1&~~0 &0&|&~~2&0&-1\\ 0&~~1&0&|&~~5&1&~~0\\ 0&-1&1&|&-5&0&~~3\end{pmatrix}.\]

Next, I’ll add row 2 to row 3. So in mathematical form, it will be:

  \[\text{Row}~3 +~\text{Row}~ 2.\]

Now I get the resultant matrix as

  \[ [\textbf{A}\qquad \textbf{I}]= \begin{pmatrix} 1&0 &0&|&2&0&-1\\ 0&1&0&|&5&1&~~0\\ 0&0&1&|&0&1&~~3\end{pmatrix}.\]

As I can see, the unit matrix \textbf{I} is on the left-hand side of the matrix [\textbf{A}\qquad \textbf{I}].

So this means the right-hand side matrix is the inverse of the matrix 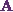\textbf{A}.

Thus the inverse of the matrix \textbf{A} is 

  \[ \textbf{A}^{-1}= \begin{pmatrix} 2&0&-1\\ 5&1&~~0\\ 0&1&~~3\end{pmatrix}.\]

Hence I can conclude that this is the answer to this example.

Now comes my other example.

 EXAMPLE 2

According to Kreyszig (2005)*, “Find the inverse by Gauss-Jordan.

  \[ \begin{pmatrix} 1&~~2&5\\ 0&-1&2\\ 2&~~4&10 \end{pmatrix} .\]

”

SOLUTION

Now here the given matrix is 

  \[ \begin{pmatrix} 1&~~2&5\\ 0&-1&2\\ 2&~~4&10 \end{pmatrix} .\]

First of all, I’ll give it a name, say \textbf{A}. Therefore the given matrix is 

  \[ \textbf{A} = \begin{pmatrix} 1&~~2&5\\ 0&-1&2\\ 2&~~4&10 \end{pmatrix} .\]

Now I’ll use the Gauss-Jordan method to find out the inverse of the matrix \textbf{A}.

As per the Gauss-Jordan method, I’ll include the unit matrix \textbf{I} on the right-hand side like 

  \[ [\textbf{A}\qquad \textbf{I}]= \begin{pmatrix} 1&~~2 &5&|&1&0&0\\ 0&-1&2&|&0&1&0\\ 2&~~4&10&|&0&0&1 \end{pmatrix}.\]

And my aim is to bring the unit matrix on the left-hand side. As per the Gauss-Jordan method, the matrix on the right-hand side will be the inverse of the matrix \textbf{A}.

STEP 1

First of all, I’ll subtract twice row 1 from row 3.

In mathematical form, I’ll write like:

  \[\text{Row}~ 3 - 2~\text{Row}~ 1.\]

So the resultant matrix is 

  \[ [\textbf{A}\qquad \textbf{I}]= \begin{pmatrix} 1&~~2 &5&|&~1&0&0\\ 0&-1&2&|&~0&1&0\\ 0&~~0&0&|&-2&0&1 \end{pmatrix}.\]

As I can see the last row of the left-hand side matrix has all zero, I can’t calculate further.

Hence the conclusion is that this matrix doesn’t have an inverse. And this is the answer to this example.

And now comes my last example.

 EXAMPLE 3

According to Kreyszig (2005)*, “Find the inverse by Gauss-Jordan.

  \[ \begin{pmatrix} ~~1&~~2&-9\\ -2&-4&~19\\ ~~0&-1&~~2 \end{pmatrix} .\]

”

SOLUTION

Now here the given matrix is 

  \[ \begin{pmatrix} ~~1&~~2&-9\\ -2&-4&~19\\ ~~0&-1&~~2 \end{pmatrix} .\]

First of all, I’ll give it a name, say 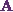\textbf{A}. Therefore the given matrix is 

  \[ \textbf{A} = \begin{pmatrix} ~~1&~~2&-9\\ -2&-4&~19\\ ~~0&-1&~~2 \end{pmatrix} .\]

Now I’ll use the Gauss-Jordan method to find out the inverse of the matrix 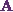\textbf{A}.

As per the Gauss-Jordan method, I’ll include the unit matrix \textbf{I} on the right-hand side like 

  \[ [\textbf{A}\qquad \textbf{I}]= \begin{pmatrix} ~~1&~~2 & -9&|&1&0&0\\ -2&-4&~19&|&0&1&0\\ ~~0&-1&~~2&|&0&0&1 \end{pmatrix}.\]

And my aim is to bring the unit matrix on the left-hand side. As per the Gauss-Jordan method, the matrix on the right-hand side will be the inverse of the matrix 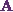\textbf{A}.

STEP 1

First of all, I’ll add twice row 1 to row 2.

In mathematical form, I’ll write like:

  \[\text{Row}~ 2 + 2~ \text{Row}~ 1.\]

So the resultant matrix is 

  \[ [\textbf{A}\qquad \textbf{I}]= \begin{pmatrix} 1&~~2 &-9&|&1&0&0\\ 0&~~0&~~1&|&2&1&0\\ 0&-1&~~2&|&0&0&1 \end{pmatrix}.\]

Now I’ll interchange row 2 and 3 to get the resultant matrix as 

  \[ [\textbf{A}\qquad \textbf{I}]= \begin{pmatrix} 1&~~2 &-9&|&1&0&0\\ 0&-1&~~2&|&0&0&1\\ 0&~~0&~~1&|&2&1&0 \end{pmatrix}.\]

As I can see, I have already got the identity matrix component in the third row.

Now I’ll try to bring the other two as well.

STEP 2

Next, I’ll add 9 times row 3 to row 1. Simultaneously, I’ll subtract twice row 3 from row 2.

In mathematical form, I’ll write like:

  \[\text{Row}~ 1 + 9~ \text{Row}~ 3, ~~~\text{Row}~ 2 - 2~\text{Row}~ 3.\]

Then the resultant matrix is 

  \[ [\textbf{A}\qquad \textbf{I}]= \begin{pmatrix} 1&~~2 &0&|&~19&~~9&0\\ 0&-1&0&|&-4&-2&1\\ 0&~~0&1&|&~~2&~~1&0\end{pmatrix}.\]

Now I’ll multiply the row 2 of the matrix [\textbf{A}\qquad \textbf{I}] with (-1).

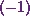So in mathematical form, it will be:

  \[\text{Row}~ 2 \times (-1).\]

Thus the resultant matrix is 

  \[ [\textbf{A}\qquad \textbf{I}]= \begin{pmatrix} 1&2 &0&|&19&9&~~0\\ 0&1&0&|&4&2&-1\\ 0&0&1&|&2&1&~~0 \end{pmatrix}.\]

Now I have got the identity matrix component at the second row as well.

Next, I’ll do that with the first row too.

STEP 3

Now I’ll subtract twice row 2 from row 1.

In mathematical form, I’ll write like:

  \[\text{Row}~ 1 - 2~\text{Row}~ 2.\]

So the resultant matrix is 

  \[ [\textbf{A}\qquad \textbf{I}]= \begin{pmatrix} 1&0 &0&|&11&5&~~2\\ 0&1&0&|&4&2&-1\\ 0&0&1&|&2&1&~~0 \end{pmatrix}.\]

As I can see, the unit matrix \textbf{I} is on the left-hand side of the matrix [\textbf{A}\qquad \textbf{I}].

So this means the right-hand side matrix is the inverse of the matrix 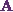\textbf{A}.

Thus the inverse of the matrix 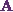\textbf{A} is 

  \[ \textbf{A}^{-1}= \begin{pmatrix} 11&5&~2\\ 4&2&-1\\ 2&1&~~0\end{pmatrix}.\]

Hence I can conclude that this is the answer to this example.