The Area Under A Parametric Curve
Suppose 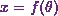 and
and 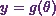 are the parametric equations of a curve. Then the
area bounded by the curve, the
are the parametric equations of a curve. Then the
area bounded by the curve, the  -axis and the ordinates
-axis and the ordinates 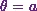 and
and 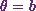 will
be
will
be
![\[\text{Area} = \int_a^b y dx.\]](4_files/image006.webp)
Now Iíll solve some examples of that.
EXAMPLE 1
According to Stroud and Booth (2013)*,
ďDetermine the area of one arch of the cycloid 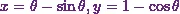 , i.e. find the area of the
plane figure bounded by the curve and the
, i.e. find the area of the
plane figure bounded by the curve and the  -axis between
-axis between 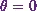 and
and  .Ē
.Ē
SOLUTION
Now here the given parametric equations of the cycloid are
![\[x = \theta - \sin \theta, y = 1 - \cos \theta.\]](4_files/image010.webp)
And I have to find out the area of the plane
figure bounded by the curve and the  -axis between
-axis between 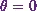 and
and  . So Iíll start with the formula
. So Iíll start with the formula
![\[\text{Area} = \int_0^{2\pi} y dx.\]](4_files/image011.webp)
STEP 1
First of all, Iíll find out the value of  in
terms of
in
terms of  . As I know the value of
. As I know the value of  is
is
![\[x = \theta - \sin \theta.\]](4_files/image014.webp)
Next, Iíll differentiate  with respect
to
with respect
to  to get
to get
![\[\frac{dx}{d\theta} = 1 - \cos \theta.\]](4_files/image016.webp)
So that gives
![\[dx = (1 - \cos \theta) d\theta.\]](4_files/image017.webp)
Therefore the area bounded by the curve and
the  -axis between
-axis between 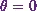 and
and  is
is
![\[\text{Area} = \int_0^{2\pi} (1 - \cos \theta) (1 - \cos \theta) d\theta.\]](4_files/image018.webp)
Then Iíll simplify it to get

As per the standard formulas in trigonometry,
![\[\cos 2 \theta = 2 \cos^2 \theta - 1.\]](4_files/image020.webp)
And that means,
![\[\cos^2 \theta = \frac{1}{2}\left(1 + \cos 2 \theta \right).\]](4_files/image021.webp)
So the area will be
![\[\text{Area} = \int_0^{2\pi} \left[ 1 + \frac{1}{2}\left(1 + \cos 2 \theta \right) - 2 \cos \theta \right]d\theta.\]](4_files/image022.webp)
Next, Iíll integrate it.
STEP 2
And for that, Iíll use the standard formulas in integration. Thus it will be
![\[\text{Area} = \left[ \theta + \frac{1}{2}\left(\theta + \frac{\sin 2 \theta}{2}\right) - 2 \sin \theta \right]_0^{2\pi}.\]](4_files/image023.webp)
Now Iíll substitute the limits to get
![\begin{eqnarray*}\text{Area} &=& \left[ 2\pi + \frac{1}{2}\left(2\pi + \frac{\sin 4\pi}{2}\right) - 2 \sin 2\pi \right]\\&& - \left[ 0 + \frac{1}{2}\left(0 + \frac{\sin 0}{2}\right) - 2 \sin 0 \right].\end{eqnarray*}](4_files/image024.webp)
As I know,  . So Iíll put these values in the
equation of the area and simplify it to get
. So Iíll put these values in the
equation of the area and simplify it to get
![\begin{eqnarray*}\text{Area} &=& \left[ 2\pi + \frac{1}{2}\left(2\pi +0\right) - 2 (0) \right]\\&& - \left[ \frac{1}{2}\left( \frac{0}{2}\right) - 0 \right]\\ &=& [2 \pi + \pi - 0]-[0]\\ &=& 3 \pi .\end{eqnarray*}](4_files/image026.webp)
Therefore the area bounded by the curve and
the  -axis between
-axis between 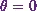 and
and  is
is  .
.
Hence I can conclude that this is the answer to the given example.
Now Iíll give another example.
EXAMPLE 2
According to Stroud and Booth (2013)*, ďThe
parametric equations of a curve are 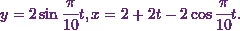 Find
the area under the curve between
Find
the area under the curve between  and
and 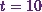 .Ē
.Ē
SOLUTION
Now here the parametric equations of a curve
are 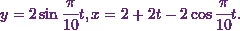 And
I have to find the area under the curve between
And
I have to find the area under the curve between  and
and 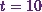 .
So Iíll start with the formula
.
So Iíll start with the formula
![\[\text{Area} = \int_0^{10} y dx.\]](4_files/image031.webp)
STEP 1
First of all, Iíll find out the value of  in
terms of
in
terms of  . As I know the value of
. As I know the value of  is
is
![\[x = 2 + 2t - 2 \cos \cfrac{\pi}{10} t.\]](4_files/image033.webp)
Next, Iíll differentiate  with respect
to
with respect
to  to get
to get
![\[\frac{dx}{dt} = 0+ 2 + 2 \sin \left(\frac{\pi}{10}t\right) \times \frac{\pi}{10}.\]](4_files/image035.webp)
So that gives
![\[dx = \left\{2 + \frac{\pi}{5}\sin \cfrac{\pi}{10}t \right\}dt.\]](4_files/image036.webp)
Therefore the area under the curve
between  and
and 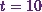 is
is
![\[\text{Area} = \int_0^{10} 2 \sin \cfrac{\pi}{10}t \left\{2 + \frac{\pi}{5}\sin \cfrac{\pi}{10}t \right\}dt.\]](4_files/image037.webp)
Then Iíll simplify it to get
![\[\text{Area} = \int_0^{10} \left\{4\sin \cfrac{\pi}{10}t + \frac{2\pi}{5}\sin^2 \cfrac{\pi}{10}t \right\}dt.\]](4_files/image038.webp)
As per the standard formulas in trigonometry,
![\[\cos 2 \theta = 1 -2 \sin^2 \theta.\]](4_files/image039.webp)
And that means,
![\[\sin^2 \theta = \frac{1}{2}\left(1 - \cos 2 \theta \right).\]](4_files/image040.webp)
So the area will be
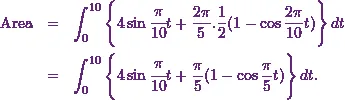
Next, Iíll integrate it.
STEP 2
And for that, Iíll use the standard formulas in integration. Thus it will be
![\[\text{Area} = \left[- 4 \cos \cfrac{\pi}{10}t \times (\frac{1}{\pi / 10}) + \frac{\pi}{5}(t - \sin \frac{\pi}{5}t \times \frac{1}{\pi/5})\right]_0^{10}.\]](4_files/image042.webp)
Now Iíll substitute the limits to get
![\begin{eqnarray*} \text{Area} &=& \left[- 4 \cos \cfrac{\pi}{10}.10\times (\frac{1}{\pi / 10}) + \frac{\pi}{5}(10 - \sin \frac{\pi}{5}.10 \times \frac{1}{\pi/5})\right]\\ && - \left[- 4 \cos \cfrac{\pi}{10}.0 \times (\frac{1}{\pi / 10}) + \frac{\pi}{5}(0 - \sin \frac{\pi}{5}.0 \times \frac{1}{\pi/5})\right]\end{eqnarray*}](4_files/image043.webp)
Then Iíll simplify it to get
![\begin{eqnarray*} \text{Area} &=& \left[- \frac{40}{\pi} \cos \pi + 2 \pi - \sin 2 \pi\right]\\ && - \left[- \frac{40}{\pi} \cos 0 + \frac{\pi}{5}( - \sin 0 \times \frac{1}{\pi/5})\right].\end{eqnarray*}](4_files/image044.webp)
As I know  and
and  . So Iíll put these values in the equation of the
area. And that gives
. So Iíll put these values in the equation of the
area. And that gives
![\[\text{Area} = \left[- \frac{40}{\pi} (-1) + 2 \pi - 0\right]- \left[- \frac{40}{\pi} (1) + \frac{\pi}{5}( - 0 . \frac{1}{\pi/5})\right].\]](4_files/image047.webp)
Now Iíll simplify it to get

Thus the area under the curve between  and
and 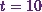 is
is  .
.