Formulas In Differentiation Applications

Suppose 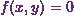f(x, y) = 0 is the equation of any curve.

So here are the first two formulas.

The equation of the tangent of this curve at the point 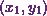(x_1, y_1) is

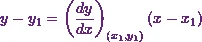
$\begin{equation*} y - y_1=\left(\frac{dy}{dx}\right)_{(x_1, y_1)}\left(x - x_1)\right. \end{equation*}$

Similarly, the equation of the normal to this curve at the point 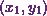(x_1, y_1) is

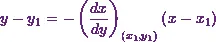
$\begin{equation*} y - y_1=- \left(\frac{dx}{dy}\right)_{(x_1, y_1)}\left(x - x_1)\right. \end{equation*}$

Now comes two more formulas.

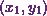Now the equation of the radius of curvature at any point (x_1, y_1) is

$R=\frac{\left[1+\left(\cfrac{dy}{dx}\right)^2\right]^{3/2}}{\cfrac{d^2y}{dx^2}}.$

The equation of the center of curvature at any point (x_1, y_1) is

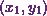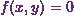Let’s say f(x, y) = 0 is a function.

For any maximum or minimum value of 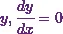$y, \cfrac{dy}{dx} = 0$ .

For the minimum value of 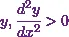$y, \cfrac{d^2y}{dx^2} > 0$ .

Also, for the maximum value of , the value of $\cfrac{dy}{dx} < 0$ .

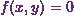Let’s say f(x, y) = 0 is a function.

For the point of inflexion, 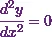$\cfrac{d^2y}{dx^2} = 0$ . Also, there will be a change of sign at 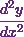$\cfrac{d^2y}{dx^2}$ when it passes through the point.