Root Mean Square Value Of A Function
Suppose 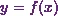 is
the equation of a curve. Then the root mean square (rms) value of the function
between
is
the equation of a curve. Then the root mean square (rms) value of the function
between  ad
ad  will be
will be
![\[\text{rms} = \sqrt{\left(\frac{1}{x_2 - x_1} \int_{x_1}^{x_2} y^2~dx\right)}.\]](2_files/image004.webp)
Now Iíll give some examples of that.
EXAMPLE 1
According to Stroud
and Booth (2013)*, ďFind the rms value of 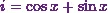 over the
range
over the
range  to
to  .Ē
.Ē
SOLUTION
Now here the given
function is 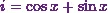 . And I have to find its
rms value over the range
. And I have to find its
rms value over the range  to
to  . Thus it
will be
. Thus it
will be
![\[\text{rms}^2 = \frac{1}{3\pi / 4 - 0} \int_{0}^{3\pi / 4} i^2~dx.\]](2_files/image008.webp)
And that means
![\[\text{rms}^2 = \frac{4}{3\pi } \int_{0}^{3\pi / 4} (\cos x + \sin x)^2~dx.\]](2_files/image009.webp)
So this gives
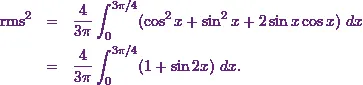
Now Iíll integrate it using the standard formulas in integration. And that means
![\[\text{rms}^2 = \frac{4}{3\pi } \left[x - \frac{\cos 2x}{2}\right]_{0}^{3\pi / 4}.\]](2_files/image011.webp)
Next, Iíll substitute the limits to get
![\[\text{rms}^2 = \frac{4}{3\pi } \left[\left(\frac{3 \pi}{4} - \frac{\cos 3 \pi /2}{2}\right)- \left(0 - \frac{\cos 0}{2}\right) \right].\]](2_files/image012.webp)
Then Iíll simplify it. And that gives
![\begin{eqnarray*} \text{rms}^2 &=& \frac{4}{3\pi }\left[\left(\frac{3 \pi}{4} - \frac{0}{2}\right) - \left( - \frac{1}{2}\right) \right]\\ &=& \frac{4}{3\pi } \left[ \frac{3 \pi}{4} - 0 +\frac{1}{2} \right] \\ &=& 1 + \frac{2}{3\pi} = 3.9439.\end{eqnarray*}](2_files/image013.webp)
Therefore the rms
value of the function  is
is
![\[\text{rms} = \sqrt{3.9439} = 1.759.\]](2_files/image015.webp)
Hence I can conclude that this is the answer to the given example.
Now Iíll give another example.
EXAMPLE 2
According to Stroud
and Booth (2013)*, ďCalculate the rms value of 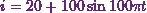 between
between  and
and 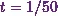 .Ē
.Ē
SOLUTION
Now here the given
function is 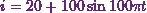 . And I have to
get its rms values between
. And I have to
get its rms values between  and
and 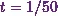 . Thus it will be
. Thus it will be
![\[\text{rms}^2 = \frac{1}{1/50 - 0} \int_{0}^{1/50} i^2~dt.\]](2_files/image019.webp)
And that means
![\[\text{rms}^2 = \frac{1}{1/50 - 0} \int_{0}^{1/50} (20 + 100 \sin 100 \pi t)^2~dt.\]](2_files/image020.webp)
So this gives
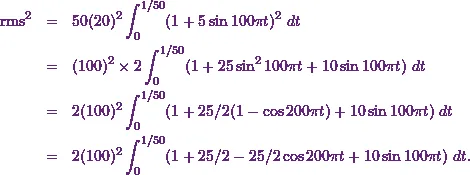
Then Iíll integrate it to get
![\[\text{rms}^2 = 2 (100)^2 \left[ t + (25/2) t - 25/2 ~\frac{\sin 200 \pi t}{200 \pi} - 10~ \frac{\cos 100 \pi t}{100 \pi}\right]_{0}^{1/50}.\]](2_files/image022.webp)
Next, Iíll substitute the limits to get
![\begin{eqnarray*} \text{rms}^2 &=& 2 (100)^2 [ \left(\frac{1}{50} + (25/2) \times\frac{1}{50} - 25/2 ~\frac{\sin 200 \pi / 50}{200 \pi} - 10~ \frac{\cos 100 \pi /50}{100 \pi}\right) \\&& - \left( 0 + (25/2) .0 - 25/2 ~\frac{\sin 200 \pi (0)}{200 \pi} - 10~ \frac{\cos 100 \pi (0)}{100 \pi} \right) ] .\end{eqnarray*}](2_files/image023.webp)
Then Iíll simplify it. So that gives
![\begin{eqnarray*}\text{rms}^2 &=& 2(100)^2 [\left(\frac{1}{50}+\frac{1}{4}-\frac{1}{16 \pi}\sin 4\pi - \frac{1}{10\pi}\cos 2 \pi\right)\\ &&-\left(0+0-0-\frac{1}{10\pi}\cos 0\right)]\\ &=& 2(100)^2 [\left(\frac{27}{100}-\frac{1}{16 \pi}.0- \frac{1}{10\pi}.1\right) + \frac{1}{10\pi}.1]\end{eqnarray*}](2_files/image024.webp)
And this is
because  .
.
Now Iíll simplify it
a bit more to get the value of  as
as
![\[\text{rms}^2 = 2 (100)^2\left [ \frac{27}{100} - \frac{1}{10\pi} + \frac{1}{10\pi}\right] = 2 (100)^2 \times \frac{27}{100}.\]](2_files/image027.webp)
So I can rewrite it as
![\[\text{rms}^2 = \frac{2\times(10)^4\times(3)^2\times(3)}{10^2}.\]](2_files/image028.webp)
And that means
![\[\text{rms}^2 = 6\times(10)^2\times(3)^2 = (30)^2 \times 6.\]](2_files/image029.webp)
Therefore the rms value of the function will be
![\[\text{rms} = \sqrt{(30)^2 \times 6} = 30\sqrt{6} = 73.485.\]](2_files/image030.webp)
Hence I can conclude that this is the answer to the given example.