Curl Of A Vector Function

 

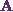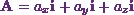Suppose I have a vector \textbf{A} such as \textbf{A} = a_x \textbf{i} + a_y \textbf{i} + a_z\textbf{i}.

Now the curl of this vector 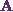\textbf{A} will be

  \[ \text{curl}~\textbf{A} = \nabla \times \textbf{A} = \left|\begin{array}{ccc} \textbf{i} & \textbf{j} &\textbf{k}\\ \cfrac{\partial}{\partial x} & \cfrac{\partial}{\partial y} & \cfrac{\partial}{\partial z}\\ a_x & a_y & a_z \end{array}\right|.\]

So if I evaluate the determinant, I’ll get the curl of this vector.

If interested, you can read more about the other posts in vector analysis like directional derivative, the gradient of a scalar field, unit normal vector, unit tangent vector and so on. Also, pretty soon I’ll write about the divergence of any vector.

Now I’ll give some examples.

EXAMPLE 1

According to Stroud and Booth (2011)*, “Show that curl (-y\textbf{i}+x\textbf{j}) is a constant vector.”

SOLUTION

Now here the given vector is (-y\textbf{i}+x\textbf{j}).

First of all, I’ll give it a name, say 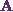\textbf{A}.

So I can say 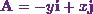\textbf{A} = -y\textbf{i}+x\textbf{j}. And this means \textbf{A} = -y\textbf{i}+x\textbf{j}+0.\textbf{k}.

Now, according to the formula for the curl of a vector, curl of the vector 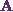\textbf{A} will be

  \[ \text{curl}~\textbf{A} = \nabla \times \textbf{A} = \left|\begin{array}{ccc} \textbf{i} & \textbf{j} &\textbf{k}\\ \cfrac{\partial}{\partial x} & \cfrac{\partial}{\partial y} & \cfrac{\partial}{\partial z}\\ -y & x &0 \end{array}\right|.\]

Next, I’ll evaluate this determinant to get the curl 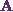\textbf{A} as

  \[\text{curl}~\textbf{A} = \textbf{i} \left[\cfrac{\partial}{\partial y}(0) - \cfrac{\partial}{\partial z} (x)\right] - \textbf{j}\left[\cfrac{\partial}{\partial x}(0)-\cfrac{\partial}{\partial z}(-y)\right]+\textbf{k}\left[\cfrac{\partial}{\partial x}(x)-\cfrac{\partial}{\partial y}(-y)\right].\]

So this gives 

  \[\text{curl}~\textbf{A} = \textbf{i} \left[0 - 0\right] - \textbf{j}\left[0-0\right]+\textbf{k}\left[1-(-1)\right].\]

Now I’ll simplify it to get

  \[\text{curl}~\textbf{A} = 2 \textbf{k}.\]

And 2 \textbf{k} is obviously a constant vector.

Hence I can prove that the curl of the vector (-y\textbf{i}+x\textbf{j}) is a constant vector.

So this is the answer to this example.

Next, I’ll give another example.

EXAMPLE 2

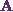According to Stroud and Booth (2011)*, “If \textbf{A} = 2xz^2\textbf{i} - xz\textbf{j} +(y+z)\textbf{k}, find curl curl \textbf{A}.”

SOLUTION

Now in this example, the given vector is \textbf{A} = 2xz^2\textbf{i} - xz\textbf{j} +(y+z)\textbf{k}.

First of all, I’ll find out the curl of the vector 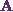\textbf{A}.

STEP 1

So the curl of the vector 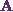\textbf{A} will be 

  \[ \text{curl}~\textbf{A} = \nabla \times \textbf{A} = \left|\begin{array}{ccc} \textbf{i} & \textbf{j} &\textbf{k}\\ \cfrac{\partial}{\partial x} & \cfrac{\partial}{\partial y} & \cfrac{\partial}{\partial z}\\ 2xz^2 & -xz &(y+z) \end{array}\right|.\]

Next, I’ll evaluate this determinant to get the curl 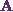\textbf{A} as

  \begin{eqnarray*}\text{curl}~\textbf{A} &=& \textbf{i} \left[\cfrac{\partial}{\partial y}(y+z) - \cfrac{\partial}{\partial z} (-xz)\right] - \textbf{j}\left[\cfrac{\partial}{\partial x}(y+z)-\cfrac{\partial}{\partial z}(2xz^2)\right]\\&&+\textbf{k}\left[\cfrac{\partial}{\partial x}(-xz)-\cfrac{\partial}{\partial y}(2xz^2)\right].\end{eqnarray*}

So this gives 

  \[\text{curl}~\textbf{A} = \textbf{i} \left[1+x\right] - \textbf{j}\left[0-4xz\right]+\textbf{k}\left[-z-0\right].\]

Now I’ll simplify it to get

  \[\text{curl}~\textbf{A} =(1+x)\textbf{i} + 4xz \textbf{j} - z \textbf{k}.\]

Next I’ll get the curl of curl 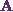\textbf{A}, that is, curl of the vector 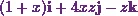(1+x)\textbf{i} + 4xz \textbf{j} - z \textbf{k}.



STEP 2

Thus curl curl 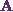\textbf{A} will be will be 

  \[ \text{curl curl}~\textbf{A} = \nabla \times \textbf{A} = \left|\begin{array}{ccc} \textbf{i} & \textbf{j} &\textbf{k}\\ \cfrac{\partial}{\partial x} & \cfrac{\partial}{\partial y} & \cfrac{\partial}{\partial z}\\ (1+x) & 4xz &-z \end{array}\right|.\]

Next, I’ll evaluate this determinant to get the curl curl 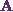\textbf{A} as

  \begin{eqnarray*}\text{curl curl}~\textbf{A} &=& \textbf{i} \left[\cfrac{\partial}{\partial y}(-z) - \cfrac{\partial}{\partial z} (4xz)\right] - \textbf{j}\left[\cfrac{\partial}{\partial x}(-z)-\cfrac{\partial}{\partial z}(1+x)\right]\\&&+\textbf{k}\left[\cfrac{\partial}{\partial x}(4xz)-\cfrac{\partial}{\partial y}(1+x)\right].\end{eqnarray*}

So this gives 

  \[\text{curl curl}~\textbf{A} = \textbf{i} \left[0-4x\right] - \textbf{j}\left[0-0\right]+\textbf{k}\left[4z-0\right].\]

Now I’ll simplify it to get

  \[\text{curl curl}~\textbf{A} =-4x\textbf{i} + 4z \textbf{k}.\]

Hence I can conclude that curl curl \textbf{A} = -4x\textbf{i} + 4z \textbf{k} is the answer to this example.