The Line Integral Of A Scalar Field
EXAMPLE 1
According to Stroud and Booth
(2011),* ďIf 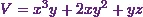 , evaluate
, evaluate 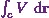 between
between 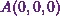 and
and 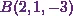 along the curve with parametric equations
along the curve with parametric equations 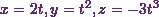 .Ē
.Ē
SOLUTION
Here the given scalar field is 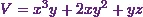 . Also the parametric equations of
. Also the parametric equations of 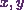 and
and  are
are 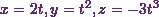 .
.
Now my first step will be to write 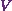 in
terms of
in
terms of 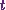 .
.
STEP 1
So, Iíll substitute 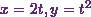 and
and  in
in 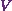 .
.
Then it will be
![\[V = (2t)^3(t^2) + 2 (2t)(t^2)^2 + (t^2)(-3t^3).\]](15_files/image012.webp)
Now Iíll simplify it. So it will be
![\[V = 8t^5 + 4t^5 - 3t^5.\]](15_files/image013.webp)
And this gives the value of 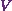 as
as
![\[V = 9t^5.\]](15_files/image014.webp)
Next Iíll get the values of 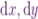 and
and 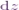 .
.
Since  , the value of
, the value of 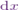 is
is
![\[ \boxed{\text{d}x = 2 \text{dt}.} \]](15_files/image019.webp)
As I know  , the value of
, the value of 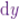 is
is
![\[ \boxed{\text{d}y = 2 t\text{dt}.} \]](15_files/image022.webp)
Also, since  , the value
of
, the value
of 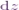 is
is
![\[ \boxed{\text{d}z = - 9 t^2\text{dt}.} \]](15_files/image024.webp)
Now I have to get the value of 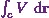 .
.
Thus in terms of 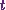 , it will be
, it will be
![\[\int_c V~\text{d}\textbf{r} = \int_c 9t^5 (\textbf{i}2\text{dt} + \textbf{j}2t\text{dt} + \textbf{k}(-9t^2)\text{dt}).\]](15_files/image025.webp)
So this means
![\[ \boxed{\int_c V~\text{d}\textbf{r} = 9 \int_c (\textbf{i} 2t^5 \text{dt} + \textbf{j} 2t^6 \text{dt} - \textbf{k} 9t^7\text{dt}) .} \]](15_files/image026.webp)
Now my next step is to find out the limits of integration.
STEP 2
Ok, so I have to integrate the scalar
field 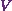 between
between 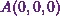 and
and 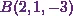 . And
that means I have to find out the value of
. And
that means I have to find out the value of 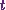 corresponding to the
points
corresponding to the
points  and
and  .
.
So, I already know that the 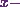 coordinate
of
coordinate
of  is
is  . Also, the parametric form of
. Also, the parametric form of  is
is  .
Then Iíll equate the
.
Then Iíll equate the 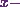 coordinate of
coordinate of  to
the parametric form of
to
the parametric form of  .
.
Thus it becomes
![\[2t = 0 \Rightarrow t = 0.\]](15_files/image033.webp)
Now Iíll check if  is
also valid for
is
also valid for 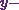 and
and  coordinates.
coordinates.
If I put  in
in  , it
becomes
, it
becomes
![\[y = (0)^2.\]](15_files/image038.webp)
So this gives the 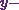 coordinate
as
coordinate
as  .
.
Similarly, I put  in
in  . And that
gives
. And that
gives
![\[z = -3(0)^3.\]](15_files/image039.webp)
So here also I get the  coordinate
as
coordinate
as  . Thus it means
. Thus it means  is the lower limit of
integration.
is the lower limit of
integration.
In the same way, now Iíll get the value
of 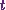 corresponding to the point
corresponding to the point  . Now the
. Now the 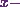 coordinate
of
coordinate
of  is
is  . Therefore I can say that
. Therefore I can say that
![\[2t = 2\]](15_files/image041.webp)
which gives 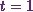 .
.
So I have two limits of integration Ė one
is  and the other is
and the other is 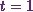 . Therefore
. Therefore 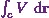 will be
will be
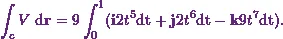
Thus my next step will be to evaluate 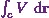 .
.
STEP 3
So I can rewrite 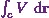 as
as
![\[\int_c V~\text{d}\textbf{r} = 9 \left[ \int_{0}^{1} \textbf{i} 2t^5 \text{dt} + \int_{0}^{1} \textbf{j} 2t^6 \text{dt} - \int_{0}^{1} \textbf{k} 9t^7\text{dt}\right].\]](15_files/image044.webp)
Now Iíll integrate this vector in the same way as the integration of a vector field. Also, Iíll follow the same rules as the rules for integration.
Hence it will be
![\[\int_c V~\text{d}\textbf{r} = 9 \left[ \frac{2t^6}{6} \textbf{i} + \frac{2t^7}{7} \textbf{j} - \frac{9t^8}{8}\textbf{k}\right]_{0}^{1}.\]](15_files/image045.webp)
Next, Iíll substitute these limits to get
![\[\int_c V~\text{d}\textbf{r} = 9 \left[ \frac{2}{6} \textbf{i} + \frac{2}{7} \textbf{j} - \frac{9}{8}\textbf{k}\right].\]](15_files/image046.webp)
And this gives
![\[\int_c V~\text{d}\textbf{r} = \left[ \frac{9 \times 2}{6} \textbf{i} + \frac{9 \times 2}{7} \textbf{j} - \frac{9 \times 9}{8}\textbf{k}\right].\]](15_files/image047.webp)
If I simplify it, Iíll get
![\[\int_c V~\text{d}\textbf{r} = 3 \textbf{i} + \frac{18}{7} \textbf{j} - \frac{81}{8}\textbf{k}.\]](15_files/image048.webp)
Hence I can conclude that this is the answer to the given example.