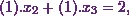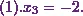Gaussian Elimination Method In 3 ◊ 3 Matrices
Suppose I have a system of equations like
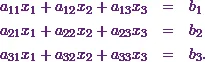
How it would be if I want to write it in a matrix form?
Well, in the matrix form, it will be
![\[ \begin{pmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{pmatrix}\begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix} = \begin{pmatrix} b_1\\ b_2\\ b_3 \end{pmatrix}. \]](14_files/image002.webp)
Here the coefficient matrix is
![\[ \begin{pmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\end{pmatrix}, \]](14_files/image003.webp)
the variable matrix is
![\[ \begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix} \]](14_files/image004.webp)
and the constant matrix is
![\[ \begin{pmatrix} b_1\\ b_2\\ b_3 \end{pmatrix}.\]](14_files/image005.webp)
Now there are several methods to solve a system of equations using matrix analysis.
One of these methods is the Gaussian elimination method.
Since here I have three equations with three variables, I will use the Gaussian elimination method in 3 ◊ 3 matrices.
If interested, you can also check out the Gaussian elimination method in 4 ◊ 4 matrices.
METHOD
In this method, first of all, I have to pick up the augmented matrix.
The augmented matrix is the combined matrix of both coefficient and constant matrices.
In this case the augmented matrix  is
is
![\[ \textbf{A}_b = \begin{pmatrix} a_{11} & a_{12} & a_{13} & b_1\\ a_{21} & a_{22} & a_{23} & b_2\\ a_{31} & a_{32} & a_{33} & b_3 \end{pmatrix}. \]](14_files/image007.webp)
Now the job is to get an equivalent upper triangular matrix.
That will be similar to
![\[ \begin{pmatrix} a_{11} & a_{12} & a_{13} & b_1\\ 0 & a & b & c\\ 0 & 0 & d & f \end{pmatrix}\text{or}~\begin{pmatrix} a_{21} & a_{22} & a_{23} & b_2\\ 0 & a & b & c\\ 0 & 0 & d & f \end{pmatrix}\]](14_files/image008.webp)
![\[ \text{or}~\begin{pmatrix} a_{31} & a_{32} & a_{33} & b_3\\ 0 & a & b & c\\ 0 & 0 & d & f \end{pmatrix}.\]](14_files/image009.webp)
After that, Iíll use the backward substitution
method to get the values of  .
.
Now Iíll give you an example.
EXAMPLE
According to Stroud and Booth (2011)* ďBy the
method of Gaussian elimination, solve the equations 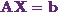 where
where
![\[ \textbf{A} = \begin{pmatrix} 1 & -2 & -4\\ 2 & 1 & -3\\ 1 & 3 & 2 \end{pmatrix}~\text{and}~\textbf{b} = \begin{pmatrix} -3\\ 4\\ 5 \end{pmatrix}. \]](14_files/image012.webp)
Ē
SOLUTION
In this example, the set of equations is 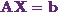 .
.
Also, I know that the coefficient matrix 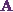 is
is
![\[ \textbf{A} = \begin{pmatrix} 1 & -2 & -4\\ 2 & 1 & -3\\ 1 & 3 & 2 \end{pmatrix}. \]](14_files/image014.webp)
In the same way, I also know that the constant
matrix  is
is
![\[ \textbf{b} = \begin{pmatrix} -3\\ 4\\ 5 \end{pmatrix}. \]](14_files/image016.webp)
Now I have to solve this set of equations.
This means I have to get the value of the matrix  .
.
Let me choose  as
as
![\[ \textbf{X} = \begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix}. \]](14_files/image018.webp)
As I have mentioned earlier, the first
step is to convert the augmented matrix  to an upper
triangular matrix.
to an upper
triangular matrix.
STEP 1
Now the augmented matrix  is
is
![\[ \textbf{A}_b = \begin{pmatrix} 1 & -2 & -4&-3\\ 2 & 1 & -3&4\\ 1 & 3 & 2&5 \end{pmatrix}. \]](14_files/image019.webp)
First of all, Iíll subtract twice row 1 from row 2.
Simultaneously, Iíll also subtract row 1 from row 3.
In mathematical term, Iíll write it like this:
Row 2 Ė 2(Row 1), Row 3 Ė Row 1.
Thus the equivalent matrix will be
![\[ \textbf{A}_b \thicksim \begin{pmatrix} 1 & -2 & -4&-3\\ 0 & 5 & 5&10\\ 0& 5 & 6&8 \end{pmatrix}. \]](14_files/image020.webp)
Next, Iíll divide row 2 by 5.
 Row 2 gives
Row 2 gives
![\[ \textbf{A}_b \thicksim \begin{pmatrix} 1 & -2 & -4&-3\\ 0 & 1 & 1&2\\ 0& 5 & 6&8 \end{pmatrix}. \]](14_files/image022.webp)
Then Iíll subtract 5 times row 2 from row 3.
Thus Row 3 Ė 5 (Row 2) gives
![\[ \textbf{A}_b \thicksim \begin{pmatrix} 1 & -2 & -4&-3\\ 0 & 1 & 1&2\\ 0& 0 & 1&-2 \end{pmatrix}. \]](14_files/image023.webp)
This is the upper triangular form of the matrix.
Therefore the system of equations in the matrix form is
![\[ \begin{pmatrix} 1 & -2 & -4\\ 0 & 1 & 1\\ 0& 0 & 1 \end{pmatrix}\begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix} = \begin{pmatrix} -3\\ 2\\ -2 \end{pmatrix}. \]](14_files/image024.webp)
Now my next job is to solve this system.
STEP 2
Here Iíll use the backward substitution to solve these equations.
This means Iíll start from the bottom.
Now the equations are
Therefore from equation (3), I can say that
![\[x_3 = -2.\]](14_files/image028.webp)
Next, Iíll substitute 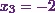 in equation
(2).
in equation
(2).
Thus it will be
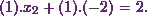
Now Iíll simplify it to get the value of 
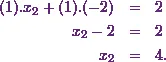
At the end, Iíll substitute 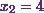 and
and 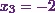 in equation
(1) to get
in equation
(1) to get
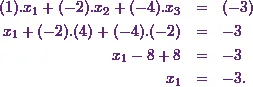
Hence I can conclude that the variable
matrix  is
is ![[-3, 4, -2]^T.](14_files/image035.webp)
This is the solution to this example.