Symmetric, Skew-Symmetric And Orthogonal Matrices
Suppose I have a matrix 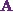 . Then
the matrix will be symmetric if the transpose of the matrix
. Then
the matrix will be symmetric if the transpose of the matrix 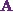 is
the same as the original matrix.
is
the same as the original matrix.
Now I give an example.
Letís say I have a matrix 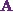 like
like
![\[ \textbf{A} = \begin{pmatrix} a_{11}&a_{12}\\ a_{21}&a_{22} \end{pmatrix}. \]](13_files/image002.webp)
Now Iíll check if itís a symmetric matrix.
First of all, Iíll transpose the matrix. And this means the first row will be the first column. Then the second row will be the second column. And it will continue in this way.
So the transpose of the matrix 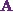 is
is  . Thus the value of
. Thus the value of  will
be
will
be
![\[ \textbf{A}^\textbf{T} = \begin{pmatrix} a_{11}&a_{21}\\ a_{12}&a_{22} \end{pmatrix}. \]](13_files/image004.webp)
Now the matrix 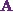 will
be
will
be
![\[ \boxed{\text{symmetric if}~\textbf{A} = \textbf{A}^\textbf{T},} \]](13_files/image005.webp)
![\[ \boxed{\text{skew-symmetric if}~\textbf{A} = -\textbf{A}^\textbf{T}} \]](13_files/image006.webp)
and
![\[ \boxed{\text{orthogonal if}~\textbf{A}^\textbf{T} = \textbf{A}^{-1}.} \]](13_files/image007.webp)
Okay, now Iíll give five different examples on symmetric, skew-symmetric and orthogonal matrices.
EXAMPLE 1
According to Kreyszig (2005)*, ďIs the following matrix symmetric, skew-symmetric, or orthogonal?
![\[ \begin{pmatrix} 3&1\\ -1&1 \end{pmatrix}. \]](13_files/image008.webp)
Ē
SOLUTION
Now here the matrix is
![\[ \begin{pmatrix} 3&1\\ -1&1 \end{pmatrix}. \]](13_files/image008.webp)
First of all, Iíll give it a name, say 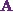 .
So it will be
.
So it will be
![\[ \textbf{A} = \begin{pmatrix} 3&1\\ -1&1 \end{pmatrix}. \]](13_files/image009.webp)
Now Iíll check whether itís a symmetric, skew-symmetric or orthogonal matrix.
STEP 1
First of all, Iíll transpose the
matrix 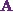 . So the first row becomes the first column. Then
the second row will be the second column. In the end, the third row will
be the third column.
. So the first row becomes the first column. Then
the second row will be the second column. In the end, the third row will
be the third column.
Thus the matrix  is
is
![\[ \textbf{A}^\textbf{T} = \begin{pmatrix} 3&-1\\ 1&1 \end{pmatrix}. \]](13_files/image010.webp)
As I can see, this is neither 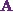 nor
nor 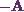 , that is
, that is
![\[ \boxed{\textbf{A}^\textbf{T} \neq \textbf{A}~\text{or}~\textbf{A}^\textbf{T} \neq-\textbf{A}.} \]](13_files/image012.webp)
So that means the matrix 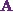 is
neither a symmetric or a skew-symmetric matrix.
is
neither a symmetric or a skew-symmetric matrix.
Next, Iíll check if itís an orthogonal matrix.
Now for that, Iíll get the inverse of the matrix 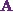 .
.
STEP 2
But I wonít use the standard way to get
the inverse of the matrix. Instead, Iíll use
the Gauss-Jordan method to find out the inverse of the matrix 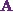 .
.
As per the Gauss-Jordan method, Iíll
include the unit matrix  on the right-hand side
like
on the right-hand side
like
![\[ [\textbf{A}\qquad \textbf{I}]= \begin{pmatrix} ~3 & 1&|&1&0\\ -1&1&|&0&1 \end{pmatrix}.\]](13_files/image014.webp)
And my aim is to bring the unit matrix on
the left-hand side. Also the matrix on the right-hand side will be the inverse
of the matrix 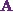 .
.
Ok, Iíll start now.
First of all, Iíll interchange row 1 and row 2 to get the equivalent matrix as
![\[ [\textbf{A}\qquad \textbf{I}] = \begin{pmatrix} -1 & 1&|&0&1\\ ~3&1&|&1&0 \end{pmatrix}.\]](13_files/image015.webp)
Now Iíll add three times row 1 with row 2. And in mathematical terms, it will be
Row 1 + 3 (Row 2).
So this gives the equivalent matrix as
![\[ [\textbf{A}\qquad \textbf{I}] = \begin{pmatrix} -1 & 1&|&0&1\\ ~0&4&|&1&3\end{pmatrix}.\]](13_files/image016.webp)
Next, Iíll divide row 2 by four.
Simultaneously, Iíll also multiply row 1 with 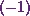 . And in
mathematical terms, it will be
. And in
mathematical terms, it will be
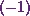 Row 1,
Row 1, 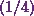 Row 2.
Row 2.
Hence the equivalent matrix matrix will be
![\[ [\textbf{A}\qquad \textbf{I}] = \begin{pmatrix} 1 & -1&|&0&-1\\ 0&~1&|&1/4&3/4\end{pmatrix}.\]](13_files/image019.webp)
Then Iíll add row 2 to row 1. And in mathematical terms, it will be
Row 1 + Row 2.
So the equivalent matrix is
![\[ [\textbf{A}\qquad \textbf{I}] = \begin{pmatrix} 1 & 0&|&1/4&-1/4\\ 0&1&|&1/4&~3/4 \end{pmatrix}.\]](13_files/image020.webp)
Now I have already got the unit matrix on
the left-hand side. So that means the inverse of the matrix 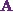 is
is
![\[ \textbf{A}^{-1} = \begin{pmatrix} 1/4&-1/4\\ 1/4&~3/4\end{pmatrix}.\]](13_files/image021.webp)
As I can see, this is not the matrix  , that is
, that is
![\[ \boxed{\textbf{A}^\textbf{T} \neq \textbf{A}^{-1}.} \]](13_files/image022.webp)
So the conclusion is that the given matrix is not an orthogonal matrix either.
CONCLUSION
As I have seen from Step 1, the given matrix is neither a symmetric or a skew-symmetric one. Also, from Step 2, I have seen that the given matrix is not an orthogonal one either.
So the conclusion is that this specific matrix is none of the symmetric, skew-symmetric or orthogonal matrices. And this is the answer to the given example.