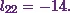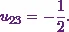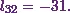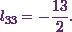Triangular Decomposition Method In 3 × 3 Matrices

There are several ways to solvrow transformation method, inverse matrix method and so on. The triangular decomposition method is also one of that.e a set of equations in matrix algebra like Gaussian elimination method,

Here I’ll only work with the 3 × 3 matrices. Soon, I’ll also write on the triangular decomposition method in 4 × 4 matrices.

Here I’ll explain how to use the row transformation method to solve a set of equations.

METHOD

Suppose I have a set of equations like

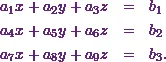
$\begin{eqnarray*} a_1x+a_2y+a_3z &=&b_1\\ a_4 x+a_5 y+a_6 z&=&b_2\\ a_7x+a_8y+a_9z &=&b_3. \end{eqnarray*}$

Now I have to solve these equations using the triangular decomposition method.

Step 1

First of all, I’ll write the set of equations in a matrix form.

Thus it will be

$\begin{pmatrix} a_1&a_2&a_3\\ a_4 &a_5 &a_6\\ a_7 &a_8 &a_9 \end{pmatrix}\begin{pmatrix} x\\ y\\ z \end{pmatrix}=\begin{pmatrix} b_1\\ b_2\\ b_3 \end{pmatrix}.$

So I can say the system of equations is in the form of 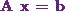$\textbf{A x = b}$ .

Here 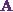$\textbf{A}$ is the coefficient matrix, $\textbf{x}$ is the variable matrix and $\textbf{b}$ is the constant matrix.

In the method of triangular decomposition, the first task is to write the coefficient matrix $\textbf{A}$ as a product of two matrices $\textbf{L}$ and $\textbf{U}$ .

The matrix $\textbf{L}$ will be a lower triangular matrix. And, the matrix $\textbf{U}$ will be an upper triangular matrix.

Thus it will be 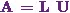$\textbf{A = L U}$ .

Here the matrix $\textbf{L}$ will look like

$\textbf{L} = \begin{pmatrix} l_{11}&0&0\\ l_{21} &l_{22} &0\\ l_{31} &l_{32} &l_{33} \end{pmatrix}.$

Similarly, the matrix $\textbf{U}$ will be

$\textbf{U} = \begin{pmatrix} 1&u_{12}&u_{13}\\ 0 &1 &u_{23}\\ 0 &0 &1 \end{pmatrix}.$

Thus the system of equations will be

$\textbf{A x = b} \Rightarrow \textbf{(L U) x = b}.$

Step 2

Now I’ll choose 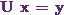$\textbf{U x = y}$ .

Here the matrix $\textbf{y}$ will be

$\textbf{y} = \begin{pmatrix} y_1\\ y_2\\ y_3 \end{pmatrix}.$

So I can say

$\textbf{A x = b} \Rightarrow \textbf{L (U x) = b} \Rightarrow \textbf{L y= b}.$

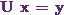Then I’ll solve for $\textbf{y}$ . Next, I’ll solve for $\textbf{x}$ using the relation $\textbf{U x = y}$ .

Now I’ll solve an example on that.

EXAMPLE OF THE TRIANGULAR DECOMPOSITION METHOD IN 3 × 3 MATRICES

Here is the example of the triangular decomposition method in 3 × 3 matrices.

EXAMPLE

According to Stroud and Booth (2011) “Using the method of triangular decomposition, solve the following set of equations.

$\begin{pmatrix} 1&4&-1\\ 4 &2 &3\\ 7 &-3 &2 \end{pmatrix}\begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix}=\begin{pmatrix} -2\\ -1\\ -18 \end{pmatrix}.$

”

SOLUTION

Here I know the set of equations as

$\begin{pmatrix} 1&4&-1\\ 4 &2 &3\\ 7 &-3 &2 \end{pmatrix}\begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix}=\begin{pmatrix} -2\\ -1\\ -18 \end{pmatrix}.$

So I can say that the coefficient matrix $\textbf{A}$ is

$\textbf{A} = \begin{pmatrix} 1&4&-1\\ 4 &2 &3\\ 7 &-3 &2 \end{pmatrix}.$

Now my first job is to write the matrix 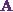$\textbf{A}$ as a product of two matrices $\textbf{L}$ and $\textbf{U}$ .

So I choose the lower triangular matrix $\textbf{L}$ as

$\textbf{L} = \begin{pmatrix} l_{11}&0&0\\ l_{21} &l_{22} &0\\ l_{31} &l_{32} &l_{33} \end{pmatrix}.$

Next, I choose the upper triangular matrix $\textbf{U}$ as

$\textbf{U} = \begin{pmatrix} 1&u_{12}&u_{13}\\ 0 &1 &u_{23}\\ 0 &0 &1 \end{pmatrix}.$

Therefore it will be $\textbf{A = LU}$ .

So that means

$\begin{pmatrix} 1&4&-1\\ 4 &2 &3\\ 7 &-3 &2 \end{pmatrix} = \begin{pmatrix} l_{11}&0&0\\ l_{21} &l_{22} &0\\ l_{31} &l_{32} &l_{33} \end{pmatrix} \begin{pmatrix} 1&u_{12}&u_{13}\\ 0 &1 &u_{23}\\ 0 &0 &1 \end{pmatrix}.$

Now I’ll get the matrices $\textbf{L}$ and $\textbf{U}$ by solving this system.

STEP 1

I’ll start with matrix multiplication.

First of all, I’ll multiply both the matrices $\textbf{L}$ and $\textbf{U}$ to get

$\begin{pmatrix} l_{11}&l_{11}u_{12}&l_{11}u_{13}\\ l_{21} &l_{21}u_{12}+l_{22} &l_{21}u_{13}+l_{22}u_{23}\\ l_{31} &l_{31}u_{12} + l_{32} &l_{31}u_{13}+ l_{32}u_{23} + l_{33} \end{pmatrix} = \begin{pmatrix} 1&4&-1\\ 4 &2 &3\\ 7 &-3 &2 \end{pmatrix} .$

So now I have nine equations to solve.

I’ll start with the first row.

STEP 2

The first one is the element from the first row and the first column.

Thus I can say

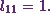
(1) $\begin{equation*} l_{11}=1. \end{equation*}$

Next, is the element from the first row and the second column.

So it will be

$l_{11}u_{12}=4.$

From equation (1), I can already say 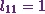$l_{11}=1$ .

Thus the value of $u_{12}$ will be

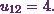
(2) $\begin{equation*} u_{12}=4. \end{equation*}$

Now comes the element from the first row and the third column.

So it will be

$l_{11}u_{13}=-1.$

From equation (1), I can already say 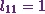$l_{11}=1$ .

Thus the value of $u_{13}$ will be

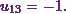
(3) $\begin{equation*} u_{13}=-1. \end{equation*}$

Now it’s time for the second row.

STEP 3

Next, comes the element from the second row and the first column.

So it will be

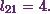
(4) $\begin{equation*} l_{21}=4. \end{equation*}$

Now comes the element from the second row and the second column.

So it will be

$l_{21}u_{12} + l_{22}=2.$

From equations (2) and (4), I can already say 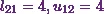$l_{21}=4, u_{12} = 4$ .

Thus the value of $l_{22}$ will be

$(4)(4) + l_{22} = 2.$

This means

(5) $\begin{equation*} l_{22}=-14. \end{equation*}$

Next, comes the element from the second row and the third column.

So it will be

$l_{21}u_{13} + l_{22}u_{23}=3.$

From equations (3), (4) and (5), I can already say 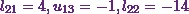$l_{21}=4, u_{13} = -1, l_{22} = -14$ .

Thus the value of $u_{23}$ will be

$(4)(-1) + (-14) u_{23} = 3.$

This means

(6) $\begin{equation*} u_{23}=-\frac{1}{2}. \end{equation*}$

Now comes the third row.

STEP 4

First comes the element from the third row and the first column.

So it will be

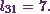
(7) $\begin{equation*} l_{31}=7. \end{equation*}$

Next comes the element from the third row and the second column.

So it will be

$l_{31}u_{12} + l_{32} = -3.$

From equations (2) and (7), I can already say 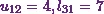$u_{12}=4, l_{31} = 7$ .

Thus the value of 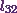$l_{32}$ will be

$(7)(4) + l_{32} = -3.$

This means

(8) $\begin{equation*} l_{32} = -31. \end{equation*}$

At the end comes the element from the third row and the third column.

So it will be

$l_{31}u_{13} + l_{32}u_{23} + l_{33} = 2.$

From equations (3), (6), (7) and (8) I can already say 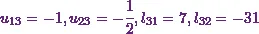$u_{13}= -1, u_{23} = -\cfrac{1}{2}, l_{31} = 7, l_{32} = -31$ .

Thus the value of 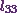$l_{33}$ will be

$(7)(-1) +(-31)\left(-\frac{1}{2}\right) + l_{33} = 2.$

This means

(9) $\begin{equation*} l_{33} = -\frac{13}{2}. \end{equation*}$

Now I’ll use equations (1) – (9) to write the matrices $\textbf{L}$ and $\textbf{U}$ .

Thus it will be

$\textbf{L} = \begin{pmatrix} 1&0&0\\ 4 &-14&0\\ 7 &-31 &-\frac{13}{2} \end{pmatrix}$

and

$\textbf{U} = \begin{pmatrix} 1&4&-1\\ 0 &1 &-\frac{1}{2}\\ 0 &0 &1 \end{pmatrix} .$

STEP 5

Now I’ll choose 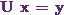$\textbf{U x = y}$ .

Here the matrix $\textbf{y}$ will be

$\textbf{y} = \begin{pmatrix} y_1\\ y_2\\ y_3 \end{pmatrix}.$

So I can say

$\textbf{A x = b} \Rightarrow \textbf{L (U x) = b} \Rightarrow \textbf{L y= b}.$

Now I’ll solve for $\textbf{y}$ .

Thus it will be

$\begin{pmatrix} 1&0&0\\ 4 &-14&0\\ 7 &-31 &-\frac{13}{2} \end{pmatrix} \begin{pmatrix} y_1\\ y_2\\ y_3 \end{pmatrix} = \begin{pmatrix} -2\\ -1\\ -18 \end{pmatrix}.$

Next I’ll do the matrix multiplication on the left-hand-side.

Therefore it will look like

$\begin{pmatrix} y_1\\ 4y_1 - 14y_2\\ 7y_1 -31y_2 - \frac{13}{2}y_ 3 \end{pmatrix} = \begin{pmatrix} -2\\ -1\\ -18 \end{pmatrix}.$

So I get three equations now.

First one is

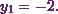
(10) $\begin{equation*} y_1 = - 2. \end{equation*}$

Next equation is

$4y_1 - 14y_2 = -1.$

Using equation (10), I can say that

$4(-2) - 14y_2 = -1.$

This gives

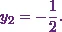
(11) $\begin{equation*} y_2 = - \frac{1}{2}. \end{equation*}$

The last equation is

$7y_1 - 31y_2 - \frac{13}{2}y_3 = -18.$

Using equations (10) and (11), I can say that

$7(-2) - 31\left(- \frac{1}{2}\right) - \frac{13}{2}y_3 = -18.$

This gives

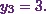
(12) $\begin{equation*} y_3 = 3. \end{equation*}$

So I can say

$\begin{pmatrix} y_1\\ y_2\\ y_3 \end{pmatrix} = \begin{pmatrix} -2\\ - \frac{1}{2}\\ 3 \end{pmatrix}.$

STEP 6

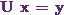Now I’ll solve for $\textbf{x}$ using the relation $\textbf{U x = y}$ .

From Step 4, I already know that the matrix $\textbf{U}$ is

$\textbf{U} = \begin{pmatrix} 1&4&-1\\ 0 &1 &-\frac{1}{2}\\ 0 &0 &1 \end{pmatrix} .$

Thus it will be

$\begin{pmatrix} 1&4&-1\\ 0 &1 &-\frac{1}{2}\\ 0 &0 &1 \end{pmatrix}\begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix} = \begin{pmatrix} -2\\ - \frac{1}{2}\\ 3 \end{pmatrix}.$

Again I’ll use matrix multiplication on the left-hand-side.

Therefore it will be

$\begin{pmatrix} x_1&4x_2&-x_3\\ 0 &x_2 &-\frac{1}{2}x_3\\ 0 &0 &x_3 \end{pmatrix} = \begin{pmatrix} -2\\ - \frac{1}{2}\\ 3 \end{pmatrix}.$

Like Step 5, here again I get three equations like

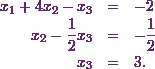
$\begin{eqnarray*} x_1 + 4x_2 - x_3 &=& - 2\\ x_2 - \frac{1}{2}x_3 &=& - \frac{1}{2}\\x_3 &=& 3. \end{eqnarray*}$

From the last equation, I already know that 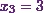x_3 = 3 .

From the middle equation, I can say that 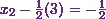$x_2 - \frac{1}{2}(3) = - \frac{1}{2}$ .

This gives 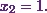x_2 = 1.

The first equation gives 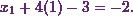x_1 + 4(1) - 3 = - 2.

This means 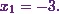x_1 = -3.

Hence I can conclude that by using the triangular decomposition method in 3 × 3 matrices I get the solution of the set of equations as

$\begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix} = \begin{pmatrix} -3\\ 1\\ 3 \end{pmatrix}.$

This is the answer to the given example.