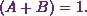Partial Fractions Of Higher Degree Numerators With Examples
EXAMPLE 1
Write the following expression into the partial fraction form:
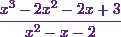 .
.
SOLUTION
Here the given expression is: 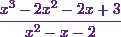 .
.
That means
the denominator is 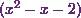 .
Also the numerator is
.
Also the numerator is 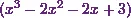 .
.
So, I can say that the degree of the numerator is 3. The denominatorís degree is 2.
This means the numeratorís degree is higher than that of the denominator. Therefore this expression has a higher degree numerator.
So, my first job is to reduce the degree of the numerator.
STEP 1
First of all, Iíll divide the numerator by the denominator.
So I can rewrite the expression as
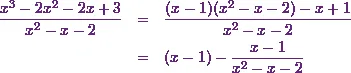
Now 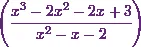 is reduced to two
parts:
is reduced to two
parts:
one is  and
and
the other is 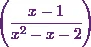 .
.
The first part cannot be reduced any more.
But I can still reduce the second part. So letís start then.
STEP 2
Here I start with the factorisation. Then I use the assumptions like
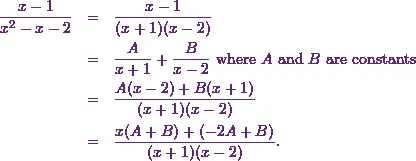
Now I have the same denominator on both left hand and right hand sides.
Therefore I can say,
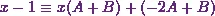 .
.
I can compare the coefficients of  on
both sides.
on
both sides.
Thus I get
I can also compare constants on both sides.
From that I have
(2) 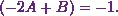
From equation (1), I have 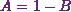 .
.
Next substitute this value of 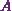 in
equation (2).
in
equation (2).
Then I get
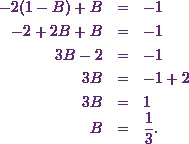
Now I substitute this value of  in
equation (1).
in
equation (1).
Therefore I have
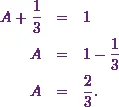
So the partial fraction of 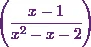 is
is 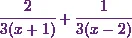 .
.
Hence I can conclude that the partial
fraction of 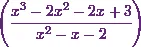 is
is 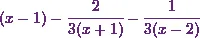 .
.
This is the solution to the given example.