Laplace Transform Of A Unit Step Function

EXAMPLE 1

According to Stroud and Booth (2011)*, “A function 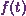f(t) is defined by

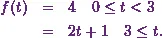
$\begin{eqnarray*} f(t) &=& 4 ~~~ 0 \leq t < 3 \\ &=& 2t + 1 ~~~ 3 \leq t.\end{eqnarray*}$

….determine its Laplace transform.”

SOLUTION

Now here I have a step function

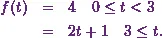
$\begin{eqnarray*} f(t) &=& 4 ~~~ 0 \leq t < 3 \\ &=& 2t + 1 ~~~ 3 \leq t.\end{eqnarray*}$

First of all, I’ll write it as a unit step function.

STEP 1

So this means

$f(t) = 4 u(t) - 4 u(t-3)+ u(t - 3) (2t + 1).$

Next, I’ll write (2t + 1) in term of (t - 3) . And that gives

$f(t) = 4 u(t) - 4 u(t - 3) + u(t - 3) \{2(t-3)+7\}.$

Then it becomes

$f(t) = 4u(t) - 4u(t-3)+u(t-3).2(t-3)+7u(t-3).$

Now I’ll simplify it to get

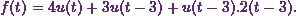
(1) $\begin{equation*} f(t) = 4u(t) +3u(t-3)+u(t-3).2(t-3). \end{equation*}$

Next, I’ll use the second-shift theorem in Laplace transform to get the Laplace transform of 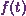f(t) .

STEP 2

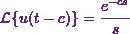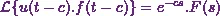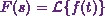Now from the standard formulas in Laplace transform, I already know that the Laplace transform of the unit step function f(t) = u (t - c) is $\mathcal{L}\{u(t-c)\} = \cfrac{e^{-cs}}{s}$ . Also, $\mathcal{L}\{u(t-c).f(t - c)\} = e^{-cs}.F(s)$ where $F(s) = \mathcal{L}\{f(t)\}$ .

As I can see from equation (1), the first term is 4u(t) . So the Laplace transform of that will be

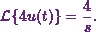
$\begin{equation*}\mathcal{L}\{4u(t)\} = \frac{4}{s}.\end{equation*}$

And the second term is 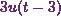3u(t-3) . So the Laplace transform of that will be

$\mathcal{L}\{3u(t-3)\} = e^{-3s} . F(s)~~~\text{where}~F(s) = \mathcal{L}\{3\}.$

And this gives

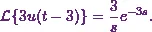
(3) $\begin{equation*} \mathcal{L}\{3u(t-3)\} = \frac{3}{s}e^{-3s}.\end{equation*}$

Then the third term is 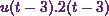u(t-3).2(t-3) . So the Laplace transform of that will be

$\mathcal{L}\{u(t-3).2(t-3)\} = e^{-3s} . F(s)~~~\text{where}~F(s) = \mathcal{L}\{2t\}.$

And that makes

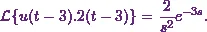
(4) $\begin{equation*} \mathcal{L}\{u(t-3).2(t-3)\} = \frac{2}{s^2}e^{-3s}.\end{equation*}$

Now I’ll combine equations (2), (3) and (4) to get the Laplace transform of the function 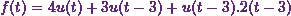f(t)= 4u(t) +3u(t-3)+u(t-3).2(t-3) as

$\mathcal{L}\{f(t)\} = \frac{4}{s}+\frac{3}{s}e^{-3s}+2\frac{e^{-3s}}{s^2}.$

Hence I can conclude that this is the answer to the given example.

Now I’ll give another example.

EXAMPLE 2

According to Stroud and Booth (2011)*, “A function 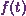f(t) is defined by

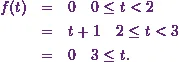
$\begin{eqnarray*} f(t) &=& 0 ~~~ 0 \leq t < 2 \\ &=& t+1 ~~~2 \leq t < 3\\ &=& 0 ~~~ 3 \leq t.\end{eqnarray*}$

Determine 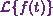$\mathcal{L}\{f(t)\}$ .”

SOLUTION

Now here I have a step function

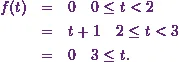
$\begin{eqnarray*} f(t) &=& 0 ~~~ 0 \leq t < 2 \\ &=& t+1 ~~~2 \leq t < 3\\ &=& 0 ~~~ 3 \leq t.\end{eqnarray*}$

First of all, I’ll write it as a unit step function like in example 1.

STEP 1

So this means

$f(t) = 0. u(t) - 0. u(t-2)+ u(t - 2) (t + 1)-u(t-3)(t+1)+0.u(t-3).$

Then I’ll simplify it to get

$f(t) = u(t - 2) (t + 1)-u(t-3)(t+1).$

Next, I’ll write (t + 1) in term of (t - 2) . And that gives

$f(t) = u(t - 2) \{(t -2)+3\}-u(t-3)(t+1).$

Now I’ll write the other (t+1) in term of (t-3) . So it becomes

$f(t) = u(t - 2) \{(t -2)+3\}-u(t-3)\{(t-3)+4\}.$

Then I’ll simplify it to get

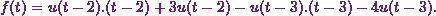
(5) $\begin{equation*}f(t) = u(t - 2) .(t -2)+3u(t - 2) -u(t-3).(t-3)-4u(t-3).\end{equation*}$

Now I’ll get the Laplace transform of this function.

STEP 2

As I can see from equation (5), the first term is u(t - 2) .(t -2) . So the Laplace transform of that will be

$\mathcal{L}\{u(t - 2) .(t -2)\} = e^{-2s}. F(s)~~~\text{where}~F(s) = \mathcal{L}\{t\}.$

And this gives

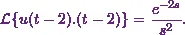
(6) $\begin{equation*} \mathcal{L}\{u(t - 2) .(t -2)\} = \frac{e^{-2s}}{s^2}.\end{equation*}$

And the second term is 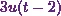3u(t-2) . So the Laplace transform of that will be

$\mathcal{L}\{3u(t-2)\} = e^{-2s} . F(s)~~~\text{where}~F(s) = \mathcal{L}\{3\}.$

And this gives

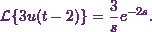
(7) $\begin{equation*} \mathcal{L}\{3u(t-2)\} = \frac{3}{s}e^{-2s}.\end{equation*}$

Then the third term is 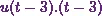u(t-3).(t-3) . So the Laplace transform of that will be

$\mathcal{L}\{u(t-3).(t-3)\} = e^{-3s} . F(s)~~~\text{where}~F(s) = \mathcal{L}\{t\}.$

And that makes

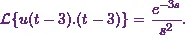
(8) $\begin{equation*} \mathcal{L}\{u(t-3).(t-3)\} = \frac{e^{-3s}}{s^2}.\end{equation*}$

In the end, comes the fourth term 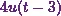4u(t-3) . So the Laplace transform of that will be

$\mathcal{L}\{4u(t-3)\} = e^{-3s} . F(s)~~~\text{where}~F(s) = \mathcal{L}\{4\}.$

And that makes

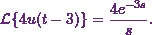
(9) $\begin{equation*} \mathcal{L}\{4u(t-3)\} = \frac{4e^{-3s}}{s}.\end{equation*}$

Now I’ll combine equations (6), (7), (8) and (9) to get the Laplace transform of the function 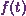f(t) as

$\mathcal{L}\{f(t)\} = \frac{e^{-2s}}{s^2} + \frac{3e^{-2s}}{s} - \frac{e^{-3s}}{s^2}-\frac{4e^{-3s}}{s}.$

Hence I can conclude that this is the answer to the given example.