Length Of Any Curve
Letís suppose 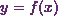 is the equation
of any curve. Then the length of the curve between
is the equation
of any curve. Then the length of the curve between  and
and  is
is
![\[S = \int_a^b \sqrt{1+\left(\cfrac{dy}{dx}\right)^2}~dx.\]](1_files/image004.webp)
EXAMPLE 1
According to Stroud and Booth (2013)*, ďFind
the length of the arc of the curve 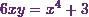 , between
, between 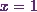 and
and  .Ē
.Ē
SOLUTION
Now here the equation of the curve is
(1) 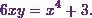
First of all, Iíll get the value of 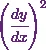 .
.
STEP 1
So, from equation (1), I can say that
the value of  is
is
![\[y = \frac{x^4+3}{6x} \Rightarrow y = \frac{x^3}{6} + \frac{1}{2x}.\]](1_files/image011.webp)
Next, Iíll differentiate  with respect
to
with respect
to  to
get
to
get
![\[\frac{dy}{dx} = \frac{3x^2}{6} - \frac{1}{2x^2}.\]](1_files/image013.webp)
Then Iíll simplify it to get
![\[\frac{dy}{dx} = \frac{x^2}{2} - \frac{1}{2x^2}.\]](1_files/image014.webp)
So this means
![\[\frac{dy}{dx} = \frac{1}{2} \left(x^2 - \frac{1}{x^2}\right).\]](1_files/image015.webp)
Therefore the value of 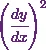 is
is
![\[\left(\cfrac{dy}{dx}\right)^2 = \frac{1}{4} \left(x^2 - \frac{1}{x^2}\right)^2.\]](1_files/image016.webp)
If I simplify it, Iíll get
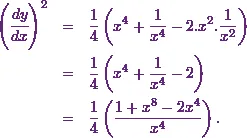
Next, Iíll get the value of 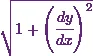 .
.
STEP 2
At first, Iíll get the value of 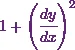 .
.
Thus it will be
![\[1+\left(\cfrac{dy}{dx}\right)^2 = 1 +\frac{1+x^8-2x^4}{4x^4}.\]](1_files/image020.webp)
Now Iíll simplify it to get
![\[1+\left(\cfrac{dy}{dx}\right)^2 = \frac{4x^4+1+x^8-2x^4}{4x^4}.\]](1_files/image021.webp)
So this gives
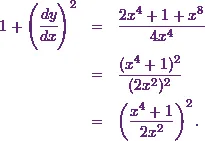
Therefore the value of 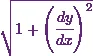 is
is
![\[\sqrt{1+\left(\cfrac{dy}{dx}\right)^2} = \frac{x^4+1}{2x^2}.\]](1_files/image023.webp)
And that means
![\[\sqrt{1+\left(\cfrac{dy}{dx}\right)^2} = \frac{x^2}{2}+\frac{1}{2x^2}.\]](1_files/image024.webp)
Now Iíll get the length  of the arc of
the curve
of the arc of
the curve 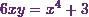 , between
, between 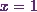 and
and  .
.
STEP 3
So it will be
![\[S = \int_1^2 \sqrt{1+\left(\cfrac{dy}{dx}\right)^2}~dx.\]](1_files/image026.webp)
And that means
![\[S = \int_1^2 \left(\frac{x^2}{2}+\frac{1}{2x^2}\right)~dx.\]](1_files/image027.webp)
Next, Iíll integrate it to get
![\[S = \left[\frac{x^3}{2.3} - \frac{1}{2x} \right]_1^2 = \left[\frac{x^3}{6} - \frac{1}{2x} \right]_1^2 .\]](1_files/image028.webp)
Then Iíll substitute the limits to get
![\[S = \left[\frac{2^3}{6} - \frac{1}{2.2} \right] - \left[\frac{1^3}{6} - \frac{1}{2.1} \right].\]](1_files/image029.webp)
Now Iíll simplify it. And that gives
![\begin{eqnarray*} S &=& \left[\frac{8}{6} - \frac{1}{4} \right] - \left[\frac{1}{6} - \frac{1}{2} \right]\\ &=& \frac{4}{3} - \frac{1}{4} - \frac{1}{6} + \frac{1}{2}\\ &=& \frac{16-3-2+6}{12}\\ &=& \frac{17}{12}.\end{eqnarray*}](1_files/image030.webp)
Thus the length of the arc is 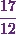 . Hence I can conclude that this is the answer to the
given example.
. Hence I can conclude that this is the answer to the
given example.
Now Iíll give another example.
EXAMPLE 2
According to Stroud and Booth (2013)*, ďFind
the length of the curve  between
between 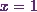 and
and  .Ē
.Ē
SOLUTION
Now here the equation of the curve is
(2) 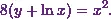
First of all, Iíll get the value of 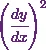 .
.
STEP 1
So Iíll differentiate equation (2)
throughout with respect to  . And that gives
. And that gives
![\[8\left(\frac{dy}{dx} + \frac{1}{x}\right) = 2x.\]](1_files/image035.webp)
Next, Iíll simplify it to get
![\[4\left(\frac{dy}{dx} + \frac{1}{x}\right) = x.\]](1_files/image036.webp)
So this means
![\[\frac{dy}{dx} + \frac{1}{x} = \frac{x}{4}.\]](1_files/image037.webp)
And that gives the value of 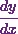 as
as
![\[\frac{dy}{dx} = \frac{x}{4} - \frac{1}{x} = \frac{x^2 - 4}{4x}.\]](1_files/image039.webp)
Now Iíll get the value of 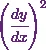 . So that will be
. So that will be
![\[\left(\cfrac{dy}{dx}\right)^2 =\frac{(x^2 - 4)^2}{(4x)^2}.\]](1_files/image040.webp)
Next, Iíll get the value of 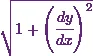 .
.
STEP 2
At first, Iíll get the value of 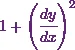 .
.
Thus it will be
![\[1+\left(\cfrac{dy}{dx}\right)^2 = 1 + \frac{(x^2 - 4)^2}{(4x)^2}.\]](1_files/image041.webp)
Now Iíll simplify it to get
![\[1+\left(\cfrac{dy}{dx}\right)^2 = \frac{(4x)^2 + (x^2 - 4)^2}{(4x)^2}.\]](1_files/image042.webp)
So this gives
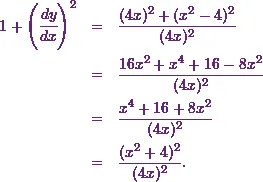
Therefore the value of 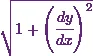 is
is
![\[\sqrt{1+\left(\cfrac{dy}{dx}\right)^2} = \frac{x^2+4}{4x}.\]](1_files/image044.webp)
And that means
![\[\sqrt{1+\left(\cfrac{dy}{dx}\right)^2} = \frac{x}{4}+ \frac{1}{x}.\]](1_files/image045.webp)
Now Iíll get the the length of the curve  between
between 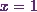 and
and  .
.
STEP 3
So it will be
![\[S = \int_1^e \sqrt{1+\left(\cfrac{dy}{dx}\right)^2}~dx.\]](1_files/image046.webp)
And that means
![\[S = \int_1^e \left(\frac{x}{4}+ \frac{1}{x}\right)~dx.\]](1_files/image047.webp)
Next, Iíll integrate it to get
![\[S = \left[\frac{x^2}{2.4} + \ln x\right]_1^{e} = \left[\frac{x^2}{8} + \ln x\right]_1^{e}.\]](1_files/image048.webp)
Then Iíll substitute the limits to get
![\[S = \left[\frac{e^2}{8} + \ln e\right] - \left[\frac{1^2}{8} + \ln 1\right].\]](1_files/image049.webp)
Now Iíll simplify it and that gives
![\begin{eqnarray*} S &=& \left[\frac{e^2}{8} + 1\right] - \left[\frac{1}{8} + 0\right]\\ &=& \frac{e^2}{8} + 1 - \frac{1}{8}\\ &=& \frac{e^2}{8} + \frac{7}{8}\\ &=& \frac{e^2 + 7}{8}. \end{eqnarray*}](1_files/image050.webp)
Thus the length of the curve is 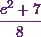 .
.
Hence I can conclude that this is the answer to the given example.