Newton’s Divided Difference Interpolation Formula

Interpolation is an estimation of a value within two known values in a sequence of values.

Newton’s divided difference interpolation formula is a interpolation technique used when the interval difference is not same for all sequence of values.

Suppose f(x0), f(x1), f(x2)………f(xn) be the (n+1) values of the function y=f(x) corresponding to the arguments x=x0, x1, x2…xn, where interval differences are not same
Then the first divided difference is given by

 

 

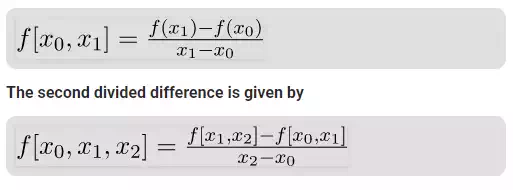
and so on…
Divided differences are symmetric with respect to the arguments i.e independent of the order of arguments.
so, 
f[x0, x1]=f[x1, x0]
f[x0, x1, x2]=f[x2, x1, x0]=f[x1, x2, x0]
By using first divided difference, second divided difference as so on .A table is formed which is called the divided difference table.

 

 

 

 

 

 

Divided difference table:
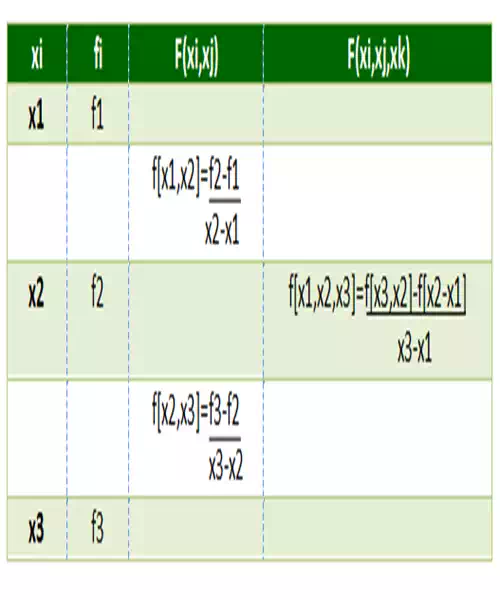
https://cdncontribute.geeksforgeeks.org/wp-content/uploads/newtonTable.webp

NEWTON’S DIVIDED DIFFERENCE INTERPOLATION FORMULA


 f(x)=f(x_0)+f[x_0, x_1]+(x-x_0)(x-x_1)f[x_0, x_1, x_2]+..........................+(x-x_0)(x-x_1)...(x-x_k)f[x_0, x_1, x_2...x_k]


Examples:

Input : Value at 7

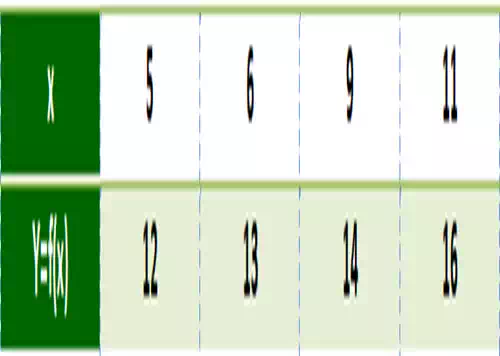
       https://cdncontribute.geeksforgeeks.org/wp-content/uploads/newton1-1.webp

Output :

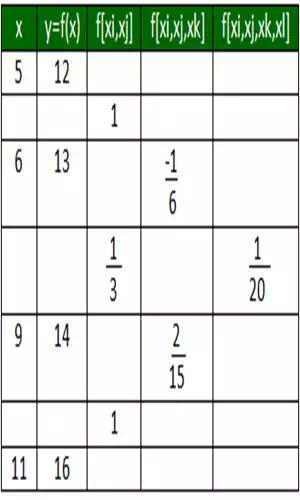
      https://cdncontribute.geeksforgeeks.org/wp-content/uploads/newton2.webp

      Value at 7 is 13.47