Mean, Variance and Standard Deviation

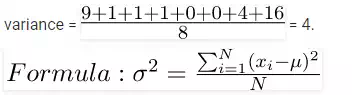
Where μ is Mean, N is the total number of elements or frequency of distribution.

Standard Deviation is square root of variance. It is a measure of the extent to which data varies from the mean.

Some Interesting Facts:

1. Value of standard deviation is 0 if all entries in input are same.

2. If we add (or subtract) a number say 7 to all values in the input set, mean is increased (or decreased) by 7, but standard deviation doesn’t change.

3. If we multiply all values in the input set by a number 7, both mean and standard deviation is multiplied by 7. But if we multiply all input values with a negative number say -7, mean is multiplied by -7, but the standard deviation is multiplied by 7.

4. Standard deviation and varience is a measure which tells how spread out numbers is. While variance gives you a rough idea of spread, the standard deviation is more concrete, giving you exact distances from the mean.

5. Mean, median and mode are the measure of central tendency of data (either grouped or ungrouped).