Unimodal functions and Bimodal functions

Unimodal Function :

A function f(x) is said to be unimodal function if for some value m it is monotonically increasing for x≤m and monotonically decreasing for x≥m. For function f(x), maximum value is f(m) and there is no other local maximum.
See figure (A) and (B):

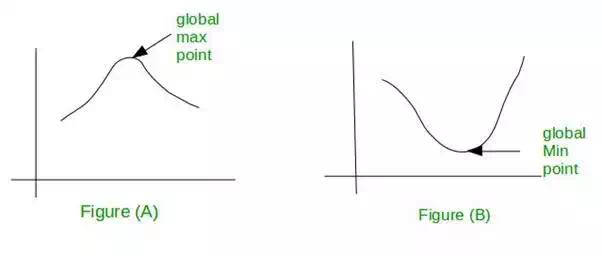
In figure (A), graph has only one maximum point and rest of the graph goes down from there and in figure (B) graph has only one minimum point and rest of the graph goes up from there. Thus, we can say that if a function has global maximum or global minimum is considered as Unimodal function.

Consider a function f(x) in the interval [a, b] and we have to determine value of x for which the function is maximised. The function strictly increase in the interval [a, x] and strictly decrease in the interval [x, b]. For this purpose we can use modified bianry search to determine the maximum or value of that function. Click here for the program.

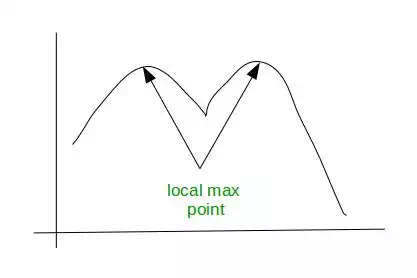
Bimodal Function :

A function is said to be bimodal function if it has two local minima or maxima. Generally bimodal function indicates two different groups. For example, In a class there are lot of students getting grade A and a lot getting grade D. This tell us that in a class there are two different group of student, one group is under-prepared and other group is over-prepared. See this figure for better understanding:

Note –

· With bimodal function and above, we don’t know if an extreme is local or global unless we know the entire graph.

· With unimodal function any extreme we find is guaranteed to be the global extreme.