Rolle’s Mean Value Theorem

Suppose f(x) be a function satisfying three conditions:

1) f(x) is continuous in the closed interval a ≤ x ≤ b

2) f(x) is differentiable in the open interval a < x < b

3) f(a) = f(b)

Then according to Rolle’s Theorem, there exists at least one point ‘c’ in the open interval (a, b) such that:

f ‘ (c) = 0

We can visualize Rolle’s theorem from the figure(1)

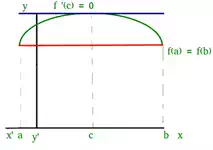
Figure(1)

In the above figure the function satisfies all three conditions given above. So, we can apply Rolle’s theorem, according to which there exists at least one point ‘c’ such that:

f ‘ (c) = 0

which means that there exists a point at which the slope of the tangent at that is equal to 0. We can easily see that at point ‘c’ slope is 0.

Similarly, there could be more than one points at which slope of tangent at those points will be 0. Figure(2) is one of the example where exists more than one point satisfying Rolle’s theorem.

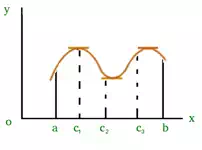
Figure(2)