Nonhomogeneous Poisson Processes

Non-homogeneous Poisson process model (NHPP) represents the number of failures experienced up to time t is a non-homogeneous Poisson process {N(t), t ≥ 0}.

The main issue in the NHPP model is to determine an appropriate mean value function to denote the expected number of failures experienced up to a certain time.
With different assumptions, the model will end up with different functional forms of the mean value function. Note that in a renewal process, the exponential assumption for the inter-arrival time between failures is relaxed, and in the NHPP, the stationary assumption is relaxed.

Non-homogeneous Poisson process model is based on the following assumptions:

–>The failure process has an independent increment, i.e. the number of failures during the time interval (t, t + s) depends on the current time t and the length of time interval s, and does not depend on the past history of the process.

–> The failure rate of the process is given by P{exactly one failure in (t, t + ∆t)} = P{N(t, t + ∆t) – N(t)=1} = (t)∆t + o(∆t) where (t) is the intensity function.

–> During a small interval ∆t, the probability of more than one failure is negligible, that is, P{two or more failure in (t, t+∆t)} = o(∆t)

–> The initial condition is N(0) = 0.

On the basis of these assumptions, the probability of exactly n failures occurring during the time interval (0, t) for the NHPP is given by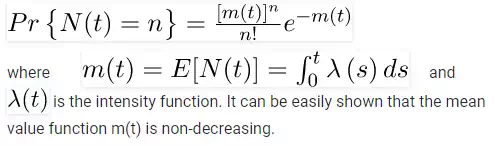

Reliability Function:
The reliability R(t), defined as the probability that there are no failures in the time interval (0, t), is given by