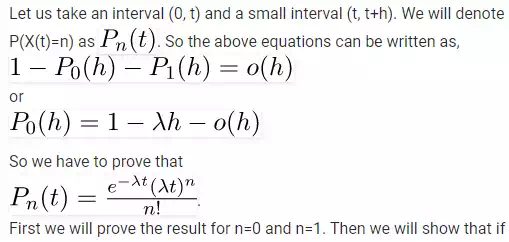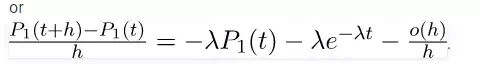Homogeneous Poisson Process

The poisson process is one of the most important and widely used processes in probability theory. It is widely used to model random points in time or space. In this article we will discuss briefly about homogenous Poisson Process.

Poisson Process –
Here we are deriving Poisson Process as a counting process. Let us assume that we are observing number of occurrence of certain event over a specified period of time. ( Here we are considering time as an example. We might also consider space etc.)We can consider them as happening under a Poisson Process provided they satisfy below conditions.

1. The number of occurrences during disjoint time intervals are independent.

2. The probability of a single occurrence during a small time interval is proportional to the length of the interval.

3. The probability of more than one occurrence during a small time interval can be neglected.

Examples –
Many real life situations can be modelled using Poisson Process. Suppose we consider number of accidents in a road. We can easily understand that the three above conditions are satisfied. For two disjoint time intervals number of accidents in a given road are independent, Again it is quite improbable that two or more accidents occur at a small interval of time. Intuitively we can also assume that probability that an accident occurs during a small interval of time is proportional to the length of the time interval. Number of earthquakes in a place can also be modelled using Poisson process.

Derivation –
Now we prove our claim that if X(t) be the number of occurrence in an interval of length t, then