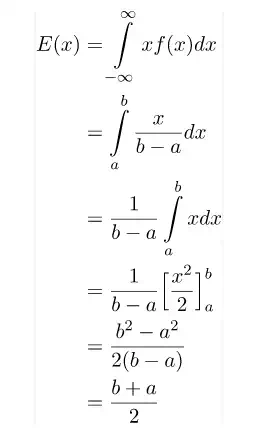Probability Distributions Set 1 (Uniform Distribution)

1. Discrete Probability Distribution – If the probabilities are defined on a discrete random variable, one which can only take a discrete set of values, then the distribution is said to be a discrete probability distribution. For example, the event of rolling a die can be represented by a discrete random variable with the probability distribution being such that each event has a probability of .

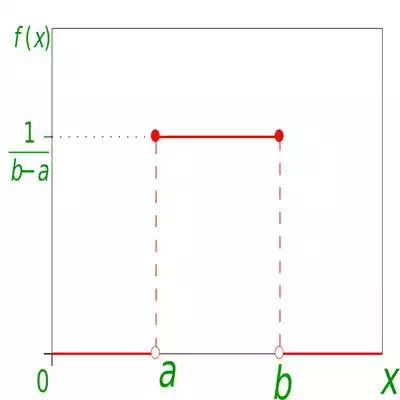
2. Continuous Probability Distribution – If the probabilities are defined on a continuous random variable, one which can take any value between two numbers, then the distribution is said to be a continuous probability distribution. For example, the temperature throughout a given day can be represented by a continuous random variable and the corresponding probability distribution is said to be continuous.

Expected or Mean Value – Using the basic definition of Expectation we get –