Mathematics | Limits, Continuity and Differentiability

1. Limits –

For a function f(x) the limit of the function at a point x=a is the value the function achieves at a point which is very close to x=a.

Formally,
Let f(x) be a function defined over some interval containing x=a, except that it
may not be defined at that point.
We say that, L = \lim_{x\to a} f(x) if there is a number \delta for every number \epsilon such that
|f(x)-L| < \epsilon whenever 0<|x-a|<\delta

The concept of limit is explained graphically in the following image –
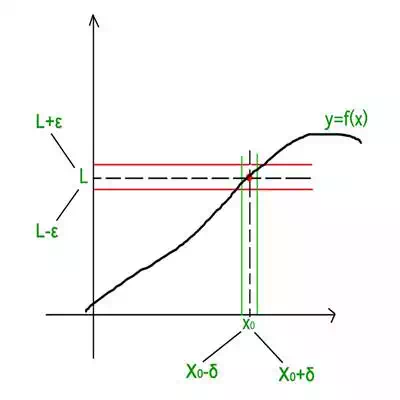
Definition of limit graphical
As is clear from the above figure, the limit can be approached from either sides of the number line i.e. the limit can be defined in terms of a number less that a or in terms of a number greater than a. Using this criteria there are two types of limits –
Left Hand Limit – If the limit is defined in terms of a number which is less than a then the limit is said to be the left hand limit. It is denoted as x\to a^- which is equivalent to x=a-h where h>0and h\to 0.
Right Hand Limit – If the limit is defined in terms of a number which is greater than a then the limit is said to be the right hand limit. It is denoted as x\to a^+ which is equivalent to x=a+h where h>0 and h\to 0.

Existence of Limit – The limit of a function f(x) at x=a exists only when its left hand limit and right hand limit exist and are equal i.e.
\lim_{x\to a^-}f(x) = \lim_{x\to a^+}f(x)

Some Common Limits –

 


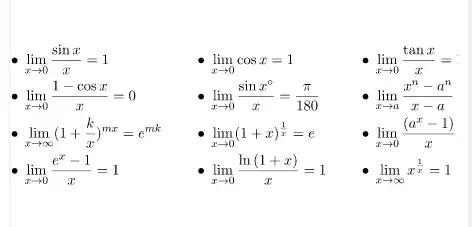
L’Hospital Rule –

 

 


Example 1 – Evaluate \lim_{x\to 0} \frac{x\cos{(x)}-\sin{(x)}}{x^2\sin{(x)}}

·         Solution – The limit is of the form \frac{0}{0}, Using L’Hospital Rule and differentiating numerator and denominator

=\:\lim_{x\to 0} \frac{\cos{(x)}-x\sin{(x)}-\cos{(x)}}{x^2\cos{(x)} + 2x\sin{(x)}}

=\:\frac{-1}{1 + 2*1}

=\:\frac{-1}{3}

·         Example 2 – Evaluate \lim_{x\to 0}\frac{a^{mx}-b^{nx}}{\sin {kx}}

·         Solution – On multiplying and dividing by kx and re-writing the limit we get –
=\:\lim_{x\to 0}\frac{(a^{mx}-1) - (b^{nx}-1)}{kx}.\frac{kx}{\sin {kx}}

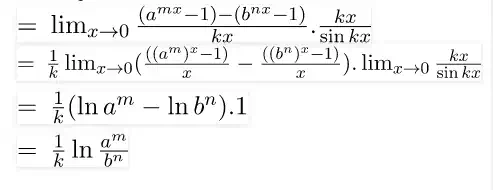
2. Continuity –

·         Example 1 – For what value of \lambda is the function defined by

  

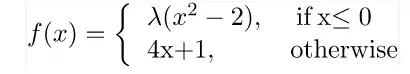
continuous at x=0?

·         Solution – For the function to be continuous the left hand limit, right hand limit and the value of the function at that point must be equal.

·        

 



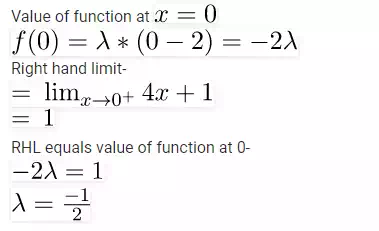
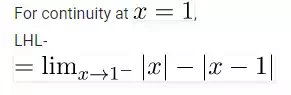
3. Differentiability –