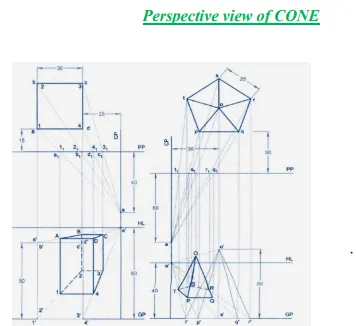
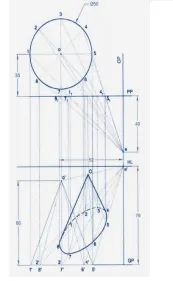
Perspective Projection

The perspective projection, also sometimes called scenographic projection or central projection, is the form of pictorial drawing which most nearly approaches the pictures as seen by the eyes.

Perspective projection is sometimes called scenographic projection or central projection, since the lines of sight converge to a single point or centre. Perspective obtained will depend on the relative position of the object, picture plane and point of sight. In this projection, the eye is assumed to be situated at a definite position relative to the object. The picture plane (vertical plane) is placed between the object and the eye. Visual rays from the eye to the object pierce the picture plane and form an image on it. This image is known as perspective of the object.

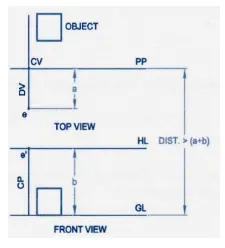
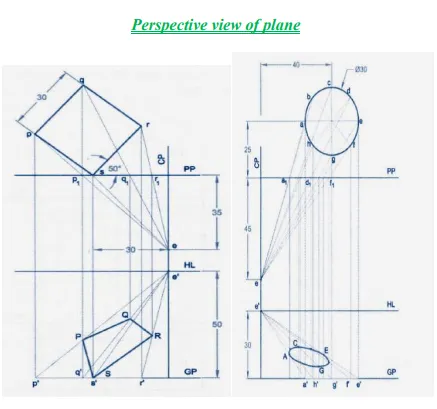
Visual Ray Method:

The points at which the visual rays joining the station point and the object pierces the picture plane in both the top and profile views, are projected to intersect each other to give points in the perspective. Since the perspective view is obtained by the intersection of the visual ray, this method is called Visual Ray Method.

Importance Point In Visual Ray Method:

1. Draw the PP line to represent the picture plane in the top view

2. Draw the plan of the object based on its position with respect to the PP

3. Draw the Ground Plane, the GP at any convenient distance from PP and project the front view based on the position of object with respect to GP.

4. Locate the position of the central plane with respect to the object and represent it as a line in both the views. On it mark the top view (s) and front view (s') of the station point based on this position with respect to PP and GP.

5. Join all plan points with s and note the intercepts of each line with PP line

6. From each intercept, with PP, draw projector vertically till it meets the line joining the elevation of the corresponding point and s' to get the perspective.

7. Follow the above step to get the perspective of other points of the object

8. Join all these points in proper sequence to get the perspective of the objective

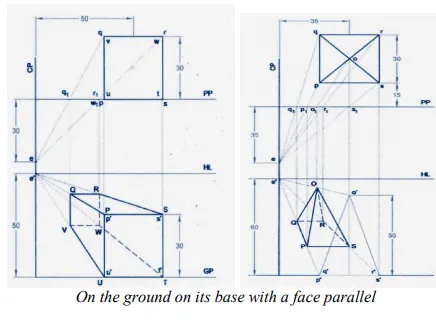
Perspective view of square prism & pyramid

(Resting on the ground on one of its faces /on the ground vertically with an edge of base parallel)