About the Presentation of the Real Types

Real floating-point numbers in C# consist of three components (according to the standard IEEE 754): sign (1 or -1), mantissa and order (exponent), and their values are calculated by a complex formula. More detailed information about the representation of the real numbers is provided in the chapter "Numeral Systems" where we will take an in-depth look at the representation of numbers and other data types in computing.

Errors in Calculations with Real Types

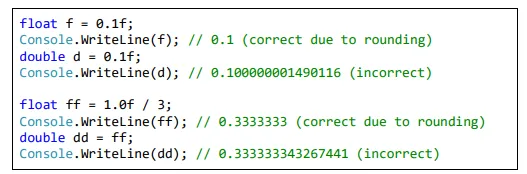
In calculations with real floating-point data types it is possible to observe strange behavior, because during the representation of a given real number it often happens to lose accuracy. The reason for this is the inability of some real numbers to be represented exactly as a sum of negative powers of the number 2. Examples of numbers that do not have an accurate representation in float and double types are for instance 0.1, 1/3, 2/7 and other. Here is a sample C# code, which demonstrates errors in calculations with floating-point numbers in C#:

The reason for the unexpected result in the first example is the fact that the number 0.1 (i.e. 1/10) has no accurate representation in the real floatingpoint number format IEEE 754 and its approximate value is recorded. When printed directly the result looks correct because of the rounding. The rounding is done during the conversion of the number to string in order to be printed on the console. When switching from float to double the approximate representation of the number in the IEEE 754 format is more noticeable. Therefore, the rounding does no longer hide the incorrect representation and we can observe the errors in it after the eighth digit.

In the second case the number 1/3 has no accurate representation and is rounded to a number very close to 0.3333333. The value of this number is clearly visible when it is written in double type, which preserves more significant digits.

Both examples show that floating-point number arithmetic can produce mistakes, and is therefore not appropriate for precise financial calculations. Fortunately, C# supports decimal precision arithmetic where numbers like 0.1 are presented in the memory without rounding.

In the example above, we declare two variables of type int, compare them and assign the result to the bool variable greaterAB. Similarly, we do the same for the variable equalA1. If the variable greaterAB is true, then A > B is printed on the console, otherwise A <= B is printed.