 It is apparent that 8 levels require three binary digits, or bits; 16 levels require four bits; and 256 levels require eight bits. In general 2n levels require n bits.
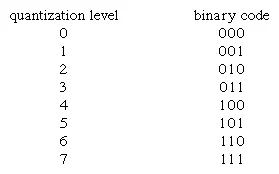
It is apparent that 8 levels require three binary digits, or bits; 16 levels require four bits; and 256 levels require eight bits. In general 2n levels require n bits.In the next step in the digitization process, the output of the quantizer is mapped into a binary sequence. An encoding table that might be used to generate the binary sequence is shown below: It is apparent that 8 levels require three binary digits, or bits; 16 levels require four bits; and 256 levels require eight bits. In general 2n levels require n bits.
It is apparent that 8 levels require three binary digits, or bits; 16 levels require four bits; and 256 levels require eight bits. In general 2n levels require n bits.
In the case of 256-level voice quantization, where each level is represented by a sequence of 8 bits, the overall rate of transmission is 8,000 samples per second times 8 bits per sample, or 64,000 bits per second. All 8 bits must be transmitted before the next sample appears. In order to use more levels, more binary samples would have to be squeezed into the allotted time slot between successive signal samples. The circuitry would become more costly, and the bandwidth of the system would become correspondingly greater. Some transmission channels (telephone wires are one example) may not have the bandwidth capability required for the increased number of binary samples and would distort the digital signals. Thus, although the accuracy required determines the number of quantization levels used, the resultant binary sequence must still be transmitted within the bandwidth tolerance allowed.
As is pointed out in analog-to-digital conversion, any available telecommunications medium has a limited capacity for data transmission. This capacity is commonly measured by the parameter called bandwidth. Since the bandwidth of a signal increases with the number of bits to be transmitted each second, an important function of a digital communications system is to represent the digitized signal by as few bits as possible—that is, to reduce redundancy. Redundancy reduction is accomplished by a source encoder, which often operates in conjunction with the analog-to-digital converter.
In general, fewer bits on the average will be needed if the source encoder takes into account the probabilities at which different quantization levels are likely to occur. A simple example will illustrate this concept. Assume a quantizing scale of only four levels: 1, 2, 3, and 4. Following the usual standard of binary encoding, each of the four levels would be mapped by a two-bit code word. But also assume that level 1 occurs 50 percent of the time, that level 2 occurs 25 percent of the time, and that levels 3 and 4 each occur 12.5 percent of the time. Using variable-bit code words might cause more efficient mapping of these levels to be achieved. The variable-bit encoding rule would use only one bit 50 percent of the time, two bits 25 percent of the time, and three bits 25 percent of the time. On average it would use 1.75 bits per sample rather than the 2 bits per sample used in the standard code.
Thus, for any given set of levels and associated probabilities, there is an optimal encoding rule that minimizes the number of bits needed to represent the source. This encoding rule is known as the Huffman code, after the American D.A. Huffman, who created it in 1952. Even more efficient encoding is possible by grouping sequences of levels together and applying the Huffman code to these sequences.
The design and performance of the Huffman code depends on the designers’ knowing the probabilities of different levels and sequences of levels. In many cases, however, it is desirable to have an encoding system that can adapt to the unknown probabilities of a source. A very efficient technique for encoding sources without needing to know their probable occurrence was developed in the 1970s by the Israelis Abraham Lempel and Jacob Ziv. The Lempel-Ziv algorithm works by constructing a codebook out of sequences encountered previously. For example, the codebook might begin with a set of four 12-bit code words representing four possible signal levels. If two of those levels arrived in sequence, the encoder, rather than transmitting two full code words (of length 24), would transmit the code word for the first level (12 bits) and then an extra two bits to indicate the second level. The encoder would then construct a new code word of 12 bits for the sequence of two levels, so that even fewer bits would be used thereafter to represent that particular combination of levels. The encoder would continue to read quantization levels until another sequence arrived for which there was no code word. In this case the sequence without the last level would be in the codebook, but not the whole sequence of levels. Again, the encoder would transmit the code word for the initial sequence of levels and then an extra two bits for the last level. The process would continue until all 4,096 possible 12-bit combinations had been assigned as code words.
In practice, standard algorithms for compressing binary files use code words of 12 bits and transmit 1 extra bit to indicate a new sequence. Using such a code, the Lempel-Ziv algorithm can compress transmissions of English text by about 55 percent, whereas the Huffman code compresses the transmission by only 43 percent.
Certain signal sources are known to produce “runs,” or long sequences of only 1s or 0s. In these cases it is more efficient to transmit a code for the length of the run rather than all the bits that represent the run itself. One source of long runs is the fax machine. A fax machine works by scanning a document and mapping very small areas of the document into either a black pixel (picture element) or a white pixel. The document is divided into a number of lines (approximately 100 per inch), with 1,728 pixels in each line (at standard resolution). If all black pixels were mapped into 1s and all white pixels into 0s, then the scanned document would be represented by 1,857,600 bits (for a standard American 11-inch page). At older modem transmission speeds of 4,800 bits per second, it would take 6 minutes 27 seconds to send a single page. If, however, the sequence of 0s and 1s were compressed using a run-length code, significant reductions in transmission time would be made.
The code for fax machines is actually a combination of a run-length code and a Huffman code; it can be explained as follows: A run-length code maps run lengths into code words, and the codebook is partitioned into two parts. The first part contains symbols for runs of lengths that are a multiple of 64; the second part is made up of runs from 0 to 63 pixels. Any run length would then be represented as a multiple of 64 plus some remainder. For example, a run of 205 pixels would be sent using the code word for a run of length 192 (3 × 64) plus the code word for a run of length 13. In this way the number of bits needed to represent the run is decreased significantly. In addition, certain runs that are known to have a higher probability of occurrence are encoded into code words of short length, further reducing the number of bits that need to be transmitted. Using this type of encoding, typical compressions for facsimile transmission range between 4 to 1 and 8 to 1. Coupled to higher modem speeds, these compressions reduce the transmission time of a single page to between 48 seconds and 1 minute 37 seconds.