Control system
Control system means by which a variable quantity or set of variable quantities is made to conform to a prescribed norm. It either holds the values of the controlled quantities constant or causes them to vary in a prescribed way. A control system may be operated by electricity, by mechanical means, by fluid pressure (liquid or gas), or by a combination of means. When a computer is involved in the control circuit, it is usually more convenient to operate all of the control systems electrically, although intermixtures are fairly common.
Development Of Control Systems.
Control systems are intimately related to the concept of automation (q.v.), but the two fundamental types of control systems, feedforward and feedback, have classic ancestry. The loom invented by Joseph Jacquard of France in 1801 is an early example of feedforward; a set of punched cards programmed the patterns woven by the loom; no information from the process was used to correct the machine’s operation. Similar feedforward control was incorporated in a number of machine tools invented in the 19th century, in which a cutting tool followed the shape of a model.
Feedback control, in which information from the process is used to correct a machine’s operation, has an even older history. Roman engineers maintained water levels for their aqueduct system by means of floating valves that opened and closed at appropriate levels. The Dutch windmill of the 17th century was kept facing the wind by the action of an auxiliary vane that moved the entire upper part of the mill. The most famous example from the Industrial Revolution is James Watt’s flyball governor of 1769, a device that regulated steam flow to a steam engine to maintain constant engine speed despite a changing load.
The first theoretical analysis of a control system, which presented a differential-equation model of the Watt governor, was published by James Clerk Maxwell, the Scottish physicist, in the 19th century. Maxwell’s work was soon generalized and control theory developed by a number of contributions, including a notable study of the automatic steering system of the U.S. battleship “New Mexico,” published in 1922. The 1930s saw the development of electrical feedback in long-distance telephone amplifiers and of the general theory of the servomechanism, by which a small amount of power controls a very large amount and makes automatic corrections. The pneumatic controller, basic to the development of early automated systems in the chemical and petroleum industries, and the analogue computer followed. All of these developments formed the basis for elaboration of control-system theory and applications during World War II, such as anti-aircraft batteries and fire-control systems.
Most of the theoretical studies as well as the practical systems up to World War II were single-loop—i.e., they involved merely feedback from a single point and correction from a single point. In the 1950s the potential of multiple-loop systems came under investigation. In these systems feedback could be initiated at more than one point in a process and corrections made from more than one point. The introduction of analogue- and digital-computing equipment opened the way for much greater complexity in automatic-control theory, an advance since labelled “modern control” to distinguish it from the older, simpler, “classical control.”
Basic Principles.
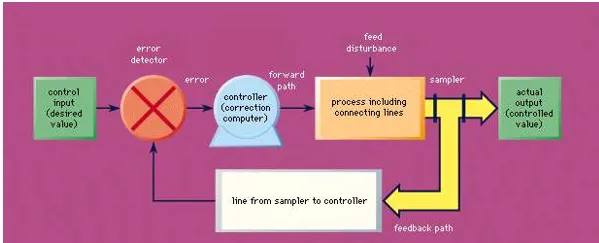
With few and relatively unimportant exceptions, all the modern control systems have two fundamental characteristics in common. These can be described as follows: (1) The value of the controlled quantity is varied by a motor (this word being used in a generalized sense), which draws its power from a local source rather than from an incoming signal. Thus there is available a large amount of power to effect necessary variations of the controlled quantity and to ensure that the operations of varying the controlled quantity do not load and distort the signals on which the accuracy of the control depends. (2) The rate at which energy is fed to the motor to effect variations in the value of the controlled quantity is determined more or less directly by some function of the difference between the actual and desired values of the controlled quantity. Thus, for example, in the case of a thermostatic heating system, the supply of fuel to the furnace is determined by whether the actual temperature is higher or lower than the desired temperature. A control system possessing these fundamental characteristics is called a closed-loop control system, or a servomechanism (see Figure). Open-loop control systems are feedforward systems.

Essential components of a typical closed-loop control system
The stability of a control system is determined to a large extent by its response to a suddenly applied signal, or transient. If such a signal causes the system to overcorrect itself, a phenomenon called hunting may occur in which the system first overcorrects itself in one direction and then overcorrects itself in the opposite direction. Because hunting is undesirable, measures are usually taken to correct it. The most common corrective measure is the addition of damping somewhere in the system. Damping slows down system response and avoids excessive overshoots or overcorrections. Damping can be in the form of electrical resistance in an electronic circuit, the application of a brake in a mechanical circuit, or forcing oil through a small orifice as in shock-absorber damping.
Another method of ascertaining the stability of a control system is to determine its frequency response—i.e., its response to a continuously varying input signal at various frequencies. The output of the control system is then compared to the input with respect to amplitude and to phase—i.e., the degree with which the input and output signals are out of step. Frequency response can be either determined experimentally—especially in electrical systems—or calculated mathematically if the constants of the system are known. Mathematical calculations are particularly useful for systems that can be described by ordinary linear differential equations. Graphic shortcuts also help greatly in the study of system responses.
Several other techniques enter into the design of advanced control systems. Adaptive control is the capability of the system to modify its own operation to achieve the best possible mode of operation. A general definition of adaptive control implies that an adaptive system must be capable of performing the following functions: providing continuous information about the present state of the system or identifying the process; comparing present system performance to the desired or optimum performance and making a decision to change the system to achieve the defined optimum performance; and initiating a proper modification to drive the control system to the optimum. These three principles—identification, decision, and modification—are inherent in any adaptive system.
Dynamic-optimizing control requires the control system to operate in such a way that a specific performance criterion is satisfied. This criterion is usually formulated in such terms that the controlled system must move from the original to a new position in the minimum possible time or at minimum total cost.
Learning control implies that the control system contains sufficient computational ability so that it can develop representations of the mathematical model of the system being controlled and can modify its own operation to take advantage of this newly developed knowledge. Thus, the learning control system is a further development of the adaptive controller.
Multivariable-noninteracting control involves large systems in which the size of internal variables is dependent upon the values of other related variables of the process. Thus the single-loop techniques of classical control theory will not suffice. More sophisticated techniques must be used to develop appropriate control systems for such processes.
There are various cases in industrial control practice in which theoretical automatic control methods are not yet sufficiently advanced to design an automatic control system or completely to predict its effects. This situation is true of the very large, highly interconnected systems such as occur in many industrial plants. In this case, operations research (q.v.), a mathematical technique for evaluating possible procedures in a given situation, can be of value.
In determining the actual physical control system to be installed in an industrial plant, the instrumentation or control-system engineer has a wide range of possible equipment and methods to use. He may choose to use a set of analogue-type instruments, those that use a continuously varying physical representation of the signal involved—i.e., a current, a voltage, or an air pressure. Devices built to handle such signals, generally called conventional devices, are capable of receiving only one input signal and delivering one output correction. Hence they are usually considered single-loop systems, and the total control system is built up of a collection of such devices. Analogue-type computers are available that can consider several variables at once for more complex control functions. These are very specific in their applications, however, and thus are not commonly used.
The number of control devices added to an industrial plant may vary widely from plant to plant. They may comprise only a few instruments that are used mainly as indicators of plant-operating conditions. The operator is thus made aware of off-normal conditions and he himself manually adjusts such plant operational devices as valves and speed regulators to maintain control. On the other hand, there may be devices of sufficient quantity and complexity so that nearly all the possible occurrences may be covered by a control-system action ensuring automatic control of any foreseeable failure or upset and thus making possible unattended control of the process.
With the development of very reliable models in the late 1960s, digital computers quickly became popular elements of industrial-plant-control systems. Computers are applied to industrial control problems in three ways: for supervisory or optimizing control; direct digital control; and hierarchy control.
In supervisory or optimizing control the computer operates in an external or secondary capacity, changing the set points in the primary plant-control system either directly or through manual intervention. A chemical process, for example, may take place in a vat the temperature of which is thermostatically regulated. For various reasons, the supervisory control system might intervene to reset the thermostat to a different level. The task of supervisory control is thus to “trim” the plant operation, thereby lowering costs or increasing production. Though the overall potential for gain from supervisory control is sharply limited, a malfunction of the computer cannot adversely affect the plant.
In direct-digital control a single digital computer replaces a group of single-loop analogue controllers. Its greater computational ability makes the substitution possible and also permits the application of more complex advanced-control techniques.
Hierarchy control attempts to apply computers to all the plant-control situations simultaneously. As such, it requires the most advanced computers and most sophisticated automatic-control devices to integrate the plant operation at every level from top-management decision to the movement of a valve.
The advantage offered by the digital computer over the conventional control system described earlier, costs being equal, is that the computer can be programmed readily to carry out a wide variety of separate tasks. In addition, it is fairly easy to change the program so as to carry out a new or revised set of tasks should the nature of the process change or the previously proposed system prove to be inadequate for the proposed task. With digital computers, this can usually be done with no change to the physical equipment of the control system. For the conventional control case, some of the physical hardware apparatus of the control system must be replaced in order to achieve new functions or new implementations of them.
Control systems have become a major component of the automation of production lines in modern factories. Automation began in the late 1940s with the development of the transfer machine, a mechanical device for moving and positioning large objects on a production line (e.g., partly finished automobile engine blocks). These early machines had no feedback control as described above. Instead, manual intervention was required for any final adjustment of position or other corrective action necessary. Because of their large size and cost, long production runs were necessary to justify the use of transfer machines.
The need to reduce the high labour content of manufactured goods, the requirement to handle much smaller production runs, the desire to gain increased accuracy of manufacture, combined with the need for sophisticated tests of the product during manufacture, have resulted in the recent development of computerized production monitors, testing devices, and feedback-controlled production robots. The programmability of the digital computer to handle a wide range of tasks along with the capability of rapid change to a new program has made it invaluable for these purposes. Similarly, the need to compensate for the effect of tool wear and other variations in automatic machining operations has required the institution of a feedback control of tool positioning and cutting rate in place of the formerly used direct mechanical motion. Again, the result is a more accurately finished final product with less chance for tool or manufacturing machine damage.