Sequences and Series

Introduction

Sequences and series have a major role to play in computational methods. In this chapter we consider various types of sequences and series, especially with respect to their convergence behavior. A series might converge “mathematically,” and yet it might not converge “numerically” (i.e., when implemented on a computer). Some of the causes of difficulties such as this will be considered here, along with possible remedies.

 Cauchy Sequences And Complete Spaces

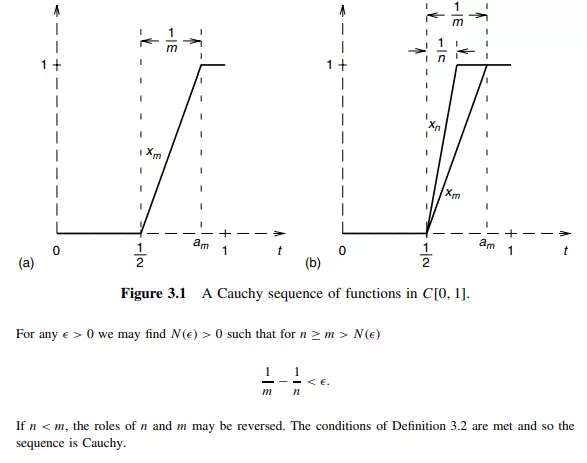
It was noted in the introduction to Chapter 1 that many computational processes are “iterative” (the Newton–Raphson method for finding the roots of an equation, iterative methods for linear system solution, etc.). The practical effect of this is to produce sequences of elements from function spaces. The sequence produced by the iterative computation is only useful if it converges. We must therefore investigate what this means.

It was possible for sequences to be either singly or doubly infinite. Here we shall assume sequences are singly infinite unless specifically stated to the contrary.

We begin with the following (standard) definition taken from Kreyszig [1, pp. 25–26].