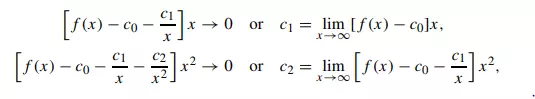Asymptotic Series

The Taylor series expansions of Section 3.5 might have a large radius of convergence, but practically speaking, if x is sufficiently far from x0, then many many terms may be needed in a computer implementation to converge to the correct solution with adequate accuracy. This is highly inefficient. Also, if many terms are to be retained, then rounding errors might accumulate and destroy the result. In other words, Taylor series approximations are really effective only for x sufficiently close to x0 (i.e., “small x”). We therefore seek expansion methods that give good approximations for large values of the argument x. These are called the asymptotic expansions, or asymptotic series. This section is just a quick introduction based mainly on Section 19.15 in Kreyszig [24]. Another source of information on asymptotic expansions, although applied mainly to problems involving differential equations, appears in Lakin and Sanchez [25].

Asymptotic expansions may take on different forms. That is, there are different “varieties” of such expansions. (This is apparent in Ref. 25.) However, we will focus on the following definition.

Definition 3.5: A series of the form