Analysis Of Discrete Linear Time Invariant (Lti/Lsi) System
1) CONVOLUTION SUM METHOD
2) DIFFERENCE EQUATION
Linear Convolution Sum Method
1. This method is powerful analysis tool for studying LSI Systems.
2. In this method we decompose input signal into sum of elementary signal. Now the elementary input signals are taken into account and individually given to the system. Now using linearity property whatever output response we get for decomposed input signal, we simply add it & this will provide us total response of the system to any given input signal.
3. Convolution involves folding, shifting, multiplication and summation operations.
4. If there are M number of samples in x(n) and N number of samples in h(n) then the maximum number of samples in y(n) is equals to M+n-1.
Linear Convolution states that
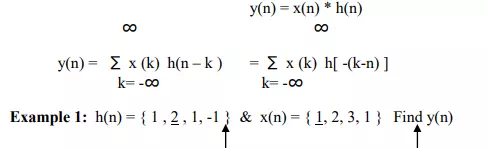
METHOD 1: GRAPHICAL REPRESENTATION
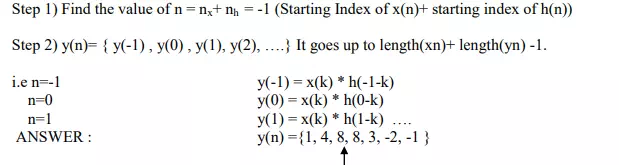
METHOD 2: MATHEMATICAL FORMULA

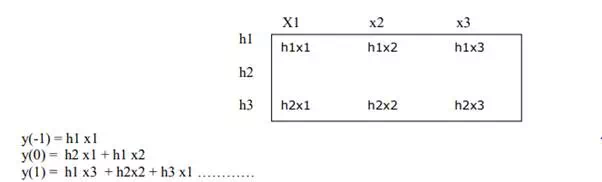
METHOD 3: VECTOR FORM (TABULATION METHOD)
![]()
METHOD 4: SIMPLE MULTIPLICATION FORM
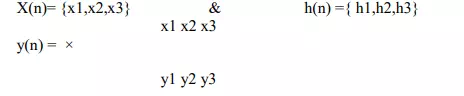
Properties Of Linear Convolution
