Application Of Dft

1. Dft For Linear Filtering

Consider that input sequence x(n) of Length L & impulse response of same system is h(n) having M samples. Thus y(n) output of the system contains N samples where N=L+M-1. If DFT of y(n) also contains N samples then only it uniquely represents y(n) in time domain. Multiplication of two DFT‘s is equivalent to circular convolution of corresponding time domain sequences. But the length of x(n) & h(n) is less than N. Hence these sequences are appended with zeros to make their length N called as ―Zero padding‖. The N point circular convolution and linear convolution provide the same sequence. Thus linear convolution can be obtained by circular convolution. Thus linear filtering is provided by DFT.

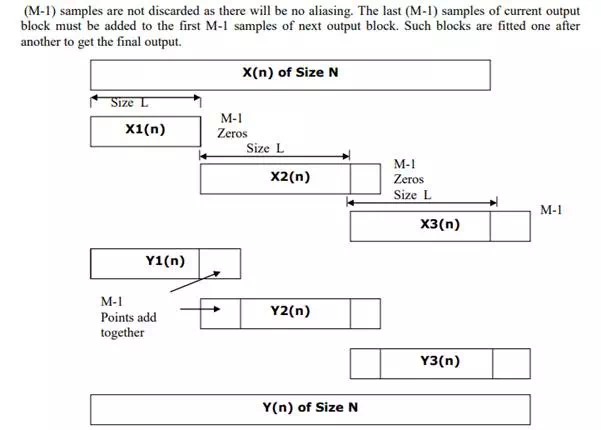
When the input data sequence is long then it requires large time to get the output sequence. Hence other techniques are used to filter long data sequences. Instead of finding the output of complete input sequence it is broken into small length sequences. The output due to these small length sequences are computed fast. The outputs due to these small length sequences are fitted one after another to get the final output response.

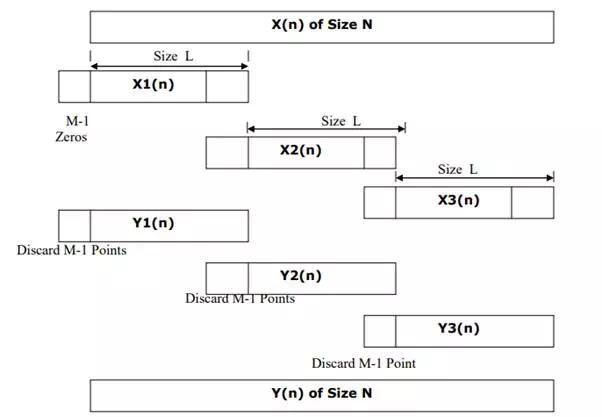
 METHOD 1: OVERLAP SAVE METHOD OF LINEAR FILTERING

Step 1> In this method L samples of the current segment and M-1 samples of the previous segment forms the input data block. Thus data block will be

METHOD 2: OVERLAP ADD METHOD OF LINEAR FILTERING