History Of Automatic Control

The use of feedback to control a system has a fascinating history. The first applications of feedback control appeared in the development of float regulator mechanisms in Greece in the period 300 to 1 B.C. [1, 2, 3].The water clock of Ktesibios used a float regulator (refer to Problem 1.11). An oil lamp devised by Philon in approximately 250 B.C. used a float regulator in an oil lamp for maintaining a constant level of fuel oil. Heron of Alexandria, who lived in the first century A.D., published a book entitled Pneumatica, which outlined several forms of water-level mechanisms using float regulators.

The first feedback system to be invented in modern Europe was the temperature regulator of Cornelis Drebbel (1572–1633) of Holland [1]. Dennis Papin [1647–1712] invented the first pressure regulator for steam boilers in 1681. Papin’s pressure regulator was a form of safety regulator similar to a pressure-cooker valve.

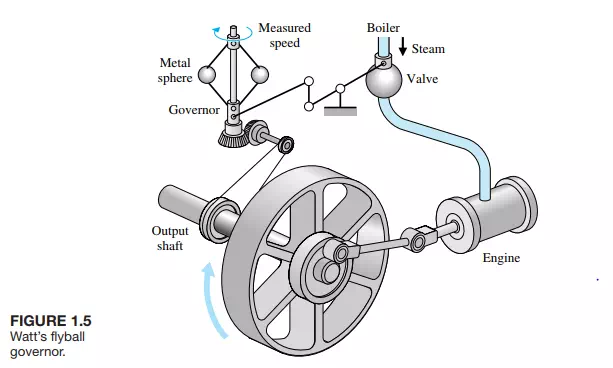
The first automatic feedback controller used in an industrial process is generally agreed to be James Watt’s flyball governor, developed in 1769 for controlling the speed of a steam engine [1, 2]. The all-mechanical device, shown in Figure 1.5, measured the speed of the output shaft and utilized the movement of the flyball with speed to control the valve and therefore the amount of steam entering the engine. As the speed increases, the ball weights rise and move away from the shaft axis, thus closing the valve. The flyweights require power from the engine to turn and therefore cause the speed measurement to be less accurate.

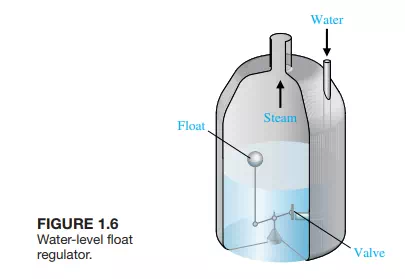
The first historical feedback system, claimed by Russia, is the water-level float regulator said to have been invented by I. Polzunov in 1765 [4]. The level regulator system is shown in Figure 1.6.The float detects the water level and controls the valve that covers the water inlet in the boiler.

The period preceding 1868 was characterized by the development of automatic control systems through intuition and invention. Efforts to increase the accuracy of the control system led to slower attenuation of the transient oscillations and even to unstable systems. It then became imperative to develop a theory of automatic control. J.C. Maxwell formulated a mathematical theory related to control theory using a differential equation model of a governor. Maxwell’s study was concerned with the effect various system parameters had on the system performance. During the same period, I. A. Vyshnegradskii formulated a mathematical theory of regulators.

Prior to World War II, control theory and practice developed in a different manner in the United States and western Europe than in Russia and eastern Europe. A main impetus for the use of feedback in the United States was the development of the telephone system and electronic feedback amplifiers by Bode, Nyquist, and Black at Bell Telephone Laboratories. The frequency domain was used primarily to describe the operation of the feedback amplifiers in terms of bandwidth and other frequency variables. In contrast, the eminent mathematicians and applied mechanicians in the former Soviet Union inspired and dominated the field of control theory. Therefore, the Russian theory tended to utilize a time-domain formulation using differential equations.

A large impetus to the theory and practice of automatic control occurred during World War II when it became necessary to design and construct automatic airplane pilots, gun-positioning systems, radar antenna control systems, and other military systems based on the feedback control approach. The complexity and expected performance of these military systems necessitated an extension of the available control techniques and fostered interest in control systems and the development of new insights and methods. Prior to 1940, for most cases, the design of control systems was an art involving a trial-and-error approach. During the 1940s, mathematical and analytical methods increased in number and utility, and control engineering became an engineering discipline in its own right .

Frequency-domain techniques continued to dominate the field of control following World War II with the increased use of the Laplace transform and the complex frequency plane. During the 1950s, the emphasis in control engineering theory was on the development and use of the s-plane methods and, particularly, the root locus approach.

Furthermore, during the 1980s, the utilization of digital computers for control components became routine.The technology of these new control elements to perform accurate and rapid calculations was formerly unavailable to control engineers. There are now over 400,000 digital process control computers installed in the United States. These computers are employed especially for process control systems in which many variables are measured and controlled simultaneously by the computer.

With the advent of Sputnik and the space age, another new impetus was imparted to control engineering. It became necessary to design complex, highly accurate control systems for missiles and space probes. Furthermore, the necessity to minimize the weight of satellites and to control them very accurately has spawned the important field of optimal control. Due to these requirements, the time-domain methods developed by Liapunov, Minorsky, and others have met with great interest in the last two decades. Recent theories of optimal control developed by L. S. Pontryagin in the former Soviet Union and R. Bellman in the United States, as well as recent studies of robust systems, have contributed to the interest in time-domain methods. It now is clear that control engineering must consider both the time-domain and the frequency-domain approaches simultaneously in the analysis and design of control systems.

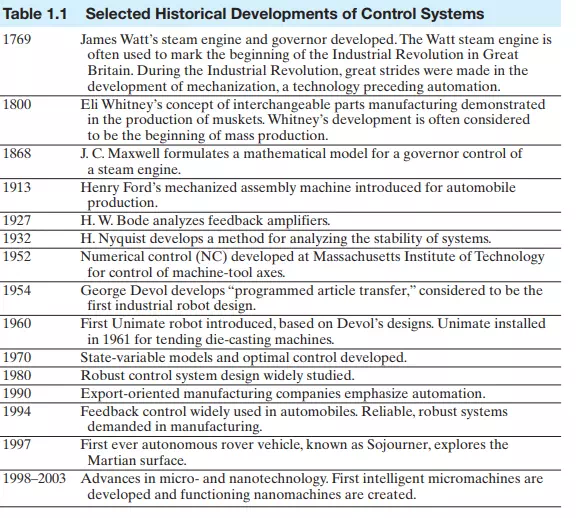
A selected history of control system development is summarized in Table 1.1.